
����Ŀ����˼���⣩
�Ķ�������龰�Ի���Ȼ�������⣺
��ʦ�������¶���һ�������Σ�����ƽ���͵��ڵ�����ƽ����2���������ν������������Σ�
С�����ȱ�������һ�������������Σ�
С������ֱ���������Ƿ���������������أ�
��1���ٸ��ݡ����������Ρ��Ķ��壬С��ó����⣺���ȱ�������һ�������������Ρ������ж�С������������Ƿ���ȷ������գ����� �����ȷ������ȷ��������Ҫ˵�����ɣ�
����ij�����ε����߳��ֱ���2��4��![]() ������ABC�������������� ����ǡ����ǡ�������Ҫ˵�����ɣ�
������ABC�������������� ����ǡ����ǡ�������Ҫ˵�����ɣ�
��2����Rt��ABC�У����߳��ֱ���a=5![]() ��c=10������������Ƿ������������Σ���˵�����ɣ�
��c=10������������Ƿ������������Σ���˵�����ɣ�
��3����Rt��ABC�У���C=90����AB=c��AC=b��BC=a����b��a����Rt��ABC�����������Σ���a��b��c��ֵ��
���𰸡���1������ȷ�����ǣ���2����cΪб��ʱ��Rt��ABC�������������Σ���bΪб��ʱ��Rt��ABC�����������Σ���3��a:b:c=![]()
��������
��1���ٸ����������������������εĶ����ж��������٣�
�ڸ����������������������εĶ������ó������
��2����c��б�ߺ�b��б������������ٸ��ݹ��ɶ����жϳ��������������Ƿ�������������εĶ��壻
��3���ȸ��ݹ��ɶ����ó�Rt��ABC����֮��Ĺ�ϵ���ٸ��ݴ������������������ο���a��ʾ��b��c��ֵ�����ɵó������
(1)����ȱ������εı߳�Ϊa��
��![]() ��
��
��ȱ�������һ�������������Σ�
�����ȱ�������һ�������������������������⣻
����ij�����ε����߳��ֱ���2��4��![]() ��
��
�������������εĶ����֪![]() ��
��
�������������������;
(2)�ٵ�cΪб��ʱ��Rt��ABC�������������Σ�
�ڵ�bΪб��ʱ��Rt��ABC�����������Σ��������£�
�����������
�ٵ�cΪб��ʱ, ![]() ��
��
��a=b��
��![]() (��
(��![]() )��
)��
��Rt��ABC��������������.
�ڵ�bΪб��ʱ![]() ��
��
��![]()
��![]()
��![]()
��Rt��ABC������������.
(3)��Rt��ABC��, ![]() ��
��
��c>b>a>0
��![]() ��
��
��Rt��ABC������������
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]()
��a:b:c=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ֣���������ѧΪ�˽�ѧ�������Ķ�����ʱ���������Ӹ��꼶ѧ������������һ����ѧ������ͳ�ƣ���������Դ˴�ͳ���������IJ�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ����Ϣ�ش��������⣺
��� | ʱ��Σ�Сʱ�� | Ƶ�� | Ƶ�� |
1 | 0��x��0.5 | 10 | 0.05 |
2 | 0.5��x��1.0 | 20 | 0.10 |
3 | 1.0��x��1.5 | 80 | b |
4 | 1.5��x��2.0 | a | 0.35 |
5 | 2.0��x��2.5 | 12 | 0.06 |
6 | 2.5��x��3.0 | 8 | 0.04 |
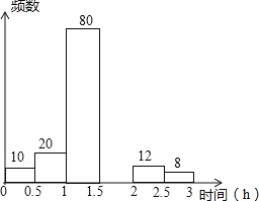
��1������a=______b=______��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�������У�ѧ�����Ķ�����ʱ�����λ�����ڵ�______�飻
��4����У����ѧ��3000�ˣ������ѧ�����Ķ���������1.5Сʱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�E��FΪ�Խ���BD�ϵ����㣬�ҡ�DAE����BCF��
��֤����1��AE��CF��
��2���ı���AECF��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
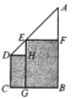
����Ŀ����ͼ�����ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �DZ�
�DZ�![]() ��һ�㣬����
��һ�㣬����![]() �ֱ���
�ֱ���![]() ��
��![]() �Ĵ��ߣ�����
�Ĵ��ߣ�����![]() ��
��![]() �Ĵ��ߣ��õ�����
�Ĵ��ߣ��õ�����![]() �;���
�;���![]() �������������ε����֮�͵����ֵ��_________��
�������������ε����֮�͵����ֵ��_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����һ�β����н�������⣺����x2 =1����x=1�� �ڷ���![]() x(x-1)=x-1�Ľ���x=2������֪���������߷ֱ�Ϊ2��9�������߳��Ƿ���x 2-14x+48=0�ĸ�������������ε��ܳ���17��19���ܷ���
x(x-1)=x-1�Ľ���x=2������֪���������߷ֱ�Ϊ2��9�������߳��Ƿ���x 2-14x+48=0�ĸ�������������ε��ܳ���17��19���ܷ���![]() �Ľ���x=3���Ծ���ÿ�������5�֣����С�������ĵ÷��ǣ���������
�Ľ���x=3���Ծ���ÿ�������5�֣����С�������ĵ÷��ǣ���������
A.0��B.5��C.10��D.15��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
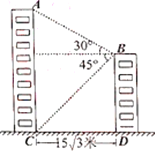
����Ŀ����ͼ��ijУ��ѧ¥![]() ��ʵ��¥
��ʵ��¥![]() ��ˮƽ���
��ˮƽ���![]() �ף���ʵ��¥����
�ף���ʵ��¥����![]() ���ý�ѧ¥����
���ý�ѧ¥����![]() ���������
���������![]() ���ײ�
���ײ�![]() ��ĸ�����
��ĸ�����![]() �����ѧ¥
�����ѧ¥![]() �ĸ߶���____�ף�����������ţ�.
�ĸ߶���____�ף�����������ţ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
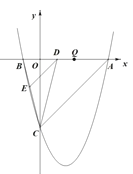
����Ŀ����֪����ͼ��������y=ax2��3ax+c(a��0)��y�ύ�ڵ�C(0����4)��x�ύ�ڵ�A��B����A������Ϊ(4��0)��
��1����������ߵĽ���ʽ��
��2����D���߶�AB�ϵĶ��㣬����D��DE��AC����BC�ڵ�E������CD������CDE��������ʱ�����D�����ꣻ
��3����ƽ����x��Ķ�ֱ��l��������߽��ڵ�P����ֱ��AC���ڵ�F����Q(2��0)���ʣ��Ƿ����������ֱ��l��ʹ�á�OQF�ǵ��������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
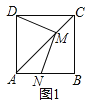
����Ŀ����ͼ1����M����������ABCD�ĶԽ���AC(�����A�غ�)�ϻ���������DM����MN��DM,��ֱ��AB��N��
(1)��֤��DM=MN��
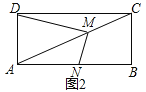
(2)����(1)�е������α�Ϊ���Σ���������������ͼ����DC=2AD����MD:MN��ֵ��
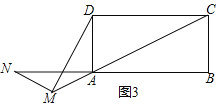
(3)��(2)�У���CD=nAD����M������CA���ӳ�����ʱ(��ͼ3)������ֱ��д��MD��MN�ı�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
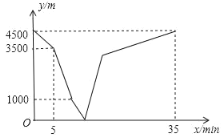
����Ŀ��Сѩ��С�ɷֱ�ӼҺ�ͼ��ݳ�������ͬһ����ֱ����·������У�Сѩ��ʼ�ܲ�����;��ij�ظ�Ϊ���У��Ҳ��е��ٶ�Ϊ�ܲ��ٶȵ�һ�룬Сѩ�ȳ���5���Ӻ�С�ɲ������г����ٻؼң�Сѩ����ͼ���ǡ������35���ӣ�����֮��ľ���y��m����Сѩ�뿪�����ص�ʱ��x��min��֮��ĺ���ͼ����ͼ��ʾ����С�ɸյ���ʱ��Сѩ��ͼ��ݵľ���Ϊ____�ף�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com