
【题目】如图所示,在△DEF中,EF=10,DF=6,DE=8,以EF的中点O为圆心,作半圆与DE相切,点A、B分别是半圆和边DF上的动点,连接AB,则AB的最大值与最小值的和是( )

A.6B.2![]() +1C.
+1C.![]() D.9
D.9
科目:初中数学 来源: 题型:
【题目】我市某企业承接了上海世博会的礼品盒制作业务,他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材.如图1所示,(单位:cm)
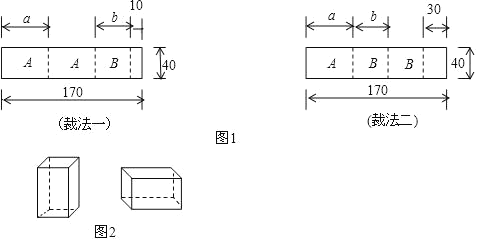
(1)列出方程(组),求出图甲中a与b的值.
(2)若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图2的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②做成的竖式和横式两种无盖礼品盒总数最多是多少个?此时横式无盖礼品盒可以做多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)已知矩形AOCD在平面直角坐标系xOy中,∠CAO=60°,OA=2,B点的坐标为(2,0),动点M以每秒2个单位长度的速度沿A→C→B运动(M点不与点A、点B重合),设运动时间为t秒.
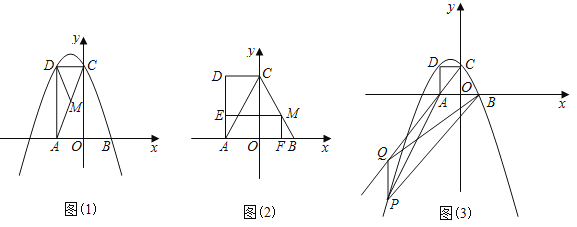
(1)求经过B、C、D三点的抛物线解析式;
(2)点P在(1)中的抛物线上,当M为AC中点时,若△PAM≌△PDM,求点P的坐标;
(3)当点M在CB上运动时,如图(2)过点M作ME⊥AD,MF⊥x轴,垂足分别为E、F,设矩形AEMF与△ABC重叠部分面积为S,求S与t的函数关系式,并求出S的最大值;
(4)如图(3)点P在(1)中的抛物线上,Q是CA延长线上的一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是![]() 的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
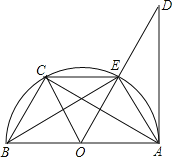
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将抛物线C1:y=x2﹣2x向左平移2个单位,向下平移3个单位得到新抛物线C2.
(1)求新抛物线C2的表达式;
(2)如图,将△OAB沿x轴向左平移得到△O′A′B′,点A(0,5)的对应点A′落在平移后的新抛物线C2上,求点B与其对应点B′的距离.
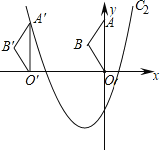
查看答案和解析>>
科目:初中数学 来源: 题型:
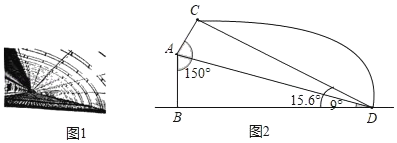
【题目】河南省政府为促进农业发展,加快农村建设,计划扶持兴建一批新型钢管装配式大棚,如图1所示线段AB、BD分别为大棚的墙高和跨度,AC表示保温板的长,已知墙高AB为3米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2所示求保温板AC的长是多少米?(精确到0.1米)(参考数据:sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校游戏节活动中,设计了一个有奖转盘游戏,如图,A转盘被分成三个面积相等的扇形,B转盘被分成四个面积相等的扇形,每一个扇形都标有相应的数字,先转动A转盘,记下指针所指区域内的数字,再转动B转盘,记下指针所指区域内的数字(当指针在边界线上时,重新转动转盘,直到指针指向一个区域内为止)
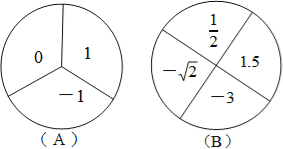
(1)请利用画树状图或列表的方法(只选其中一种),表示出转转盘可能出现的所有结果;
(2)如果将两次转转盘指针所指区域的数据相乘,乘积是无理数时获得一等奖,那么获得一等奖的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,BC=6,点D、E分别是边AB、AC上的动点(点D、E不与△ABC的顶点重合),AD和BE交于点F,且∠AFE=∠ABC

(1)求证:△ABD∽△BCE;
(2)设AE=x,ADFD=y,求y关于x的函数关系式,并直接写出x的取值范围;
(3)当△AEF是等腰三角形时,求DF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com