

·ÖĪö £Ø1£©ÓÉBC”ĪOAµĆ”ĻB+”ĻO=180”ć£¬ĖłŅŌ”ĻO=180”ć-”ĻB=80”ć£¬Ōņ”ĻA+”ĻO=180”ć£¬øł¾ŻĘ½ŠŠĻßµÄÅŠ¶Ø¼“æɵƵ½OB”ĪAC£»
£Ø2£©ÓÉOEĘ½·Ö”ĻBOFµĆµ½”ĻBOE=”ĻFOE£¬øł¾Ż”ĻFOC=”ĻAOC£¬æɵƔĻEOF+”ĻCOF=$\frac{1}{2}$”ĻAOB=40”ć£»
£Ø3£©ÓÉBC”ĪOAµĆµ½OCB=”ĻAOC£¬”ĻOFB=”ĻAOF£¬øł¾Ż”ĻFOC=”ĻAOC£¬µĆµ½”ĻAOF=2”ĻAOC£¬ĖłŅŌ”ĻOFB=2”ĻOCB£¬
£Ø4£©Éč”ĻAOCµÄ¶ČŹżĪŖx£¬Ōņ”ĻOFB=2x£¬øł¾ŻĘ½ŠŠĻߵĊŌÖŹµĆ”ĻOEB=”ĻAOE£¬Ōņ”ĻOEB=”ĻEOC+”ĻAOC=40”ć+x£¬ŌŁøł¾ŻČż½ĒŠĪÄŚ½ĒŗĶ¶ØĄķµĆ”ĻOCA=180”ć-”ĻAOC-”ĻA=80”ć-x£¬ĄūÓĆ”ĻOEB=”ĻOCAµĆµ½40”ć+x=80”ć-x£¬½āµĆx=20”ć£¬æɵƔĻOCA=80”ć-x=60”ć£®
½ā“š ½ā£ŗ£Ø1£©”ßBC”ĪOA£¬
”ą”ĻB+”ĻO=180”ć£¬
”ą”ĻO=180”ć-”ĻB=80”ć£¬
¶ų”ĻA=100”ć£¬
”ą”ĻA+”ĻO=180”ć£¬
”ąOB”ĪAC£»
£Ø2£©”ßOEĘ½·Ö”ĻBOF£¬
”ą”ĻBOE=”ĻFOE£¬
¶ų”ĻFOC=”ĻAOC£¬
”ą”ĻEOC=”ĻEOF+”ĻCOF=$\frac{1}{2}$”ĻAOB=$\frac{1}{2}$”Į80”ć=40”ć£»
£Ø3£©²»±ä£®
”ßBC”ĪOA£¬
”ą”ĻOCB=”ĻAOC£¬”ĻOFB=”ĻAOF£¬
”ß”ĻFOC=”ĻAOC£¬
”ą”ĻAOF=2”ĻAOC£¬
”ą”ĻOFB=2”ĻOCB£¬
¼“”ĻOCB£ŗ”ĻOFB=1£ŗ2£»
£Ø4£©Éč”ĻAOCµÄ¶ČŹżĪŖx£¬Ōņ”ĻOFB=2x£¬
”ß”ĻOEB=”ĻAOE£¬
”ą”ĻOEB=”ĻEOC+”ĻAOC=40”ć+x£¬
¶ų”ĻOCA=180”ć-”ĻAOC-”ĻA=180”ć-x-100”ć=80”ć-x£¬
”ß”ĻOEB=”ĻOCA£¬
”ą40”ć+x=80”ć-x£¬
½āµĆx=20”ć£¬
”ą”ĻOCA=80”ć-x=80”ć-20”ć=60”ć£®
µćĘĄ ±¾Ģāæ¼²éĘ½ŅĘŗĶĘ½ŠŠĻߵĊŌÖŹµÄÓŠ¹ŲÖŖŹ¶£®Ę½ŅʵĻł±¾ŠŌÖŹŹĒ£ŗ¢ŁĘ½ŅĘ²»øıäĶ¼ŠĪµÄŠĪדŗĶ“󊔣»¢Ś¾¹żĘ½ŅĘ£¬¶ŌÓ¦µćĖłĮ¬µÄĻ߶ĪĘ½ŠŠĒŅĻąµČ£¬¶ŌÓ¦Ļ߶ĪĘ½ŠŠĒŅĻąµČ£¬¶ŌÓ¦½ĒĻąµČ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
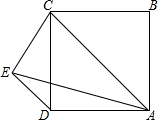 ŌŚÕż·½ŠĪABCDÖŠ£¬ACĪŖ¶Ō½ĒĻߣ¬DEĘ½ŠŠÓŚAC£¬AE=AC£¬Ēó”ĻCEDµÄ¶ČŹż£®
ŌŚÕż·½ŠĪABCDÖŠ£¬ACĪŖ¶Ō½ĒĻߣ¬DEĘ½ŠŠÓŚAC£¬AE=AC£¬Ēó”ĻCEDµÄ¶ČŹż£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
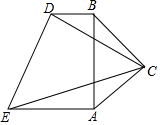 ČēĶ¼£¬ŌŚĢŻŠĪAEDBÖŠ£¬BD”ĪAE£¬”ĻABD=90”ć£¬ŌŚABµÄÓŅ²ą×÷Rt”÷ACB£¬”ĻACB=90”ć£¬AC=BC£¬ĒŅ”ĻECD=45”ć
ČēĶ¼£¬ŌŚĢŻŠĪAEDBÖŠ£¬BD”ĪAE£¬”ĻABD=90”ć£¬ŌŚABµÄÓŅ²ą×÷Rt”÷ACB£¬”ĻACB=90”ć£¬AC=BC£¬ĒŅ”ĻECD=45”ć²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
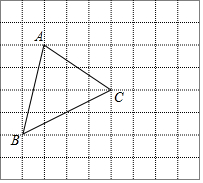 ČēĶ¼£¬”÷ABCµÄÓŠČżøö¶„µć¶¼ŌŚ±ß³¤ĪŖ1µÄŠ”Õż·½ŠĪĶųøńµÄøńµćÉĻ£®
ČēĶ¼£¬”÷ABCµÄÓŠČżøö¶„µć¶¼ŌŚ±ß³¤ĪŖ1µÄŠ”Õż·½ŠĪĶųøńµÄøńµćÉĻ£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com