
如图,在 中,AB=AC,以AB为直径的
中,AB=AC,以AB为直径的 交BC于点M,
交BC于点M, 于点N.
于点N.
(1)求证:MN是 的切线;(2)若
的切线;(2)若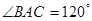 ,AB=2,求图中阴影部分的面积.
,AB=2,求图中阴影部分的面积.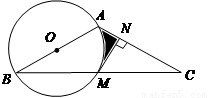
(1)证明MN是 的切线,即证明MN⊥OM,可通过证明OM∥AC,因为MN⊥AC,那么MN⊥OM,M在圆上,且OM为⊙O的半径,则说明MN是
的切线,即证明MN⊥OM,可通过证明OM∥AC,因为MN⊥AC,那么MN⊥OM,M在圆上,且OM为⊙O的半径,则说明MN是 的切线.
的切线.
(2)
【解析】
试题分析:(1)证明:连接OM.
∵AB=AC
∴∠B=∠C
∵OM=OB
∴∠B=∠OMB
∴∠C=∠OMB
∴OM∥AC
∵MN⊥AC
∴MN⊥OM
又∵M在⊙上
且OM为⊙O的半径
∴MN是⊙O的切线.
(2)连AM.
∵AB是⊙O的直径
∴∠AMB=90°
即AM⊥BC
又∵∠BAC=120°
∴∠BAM=∠CAM= ∠BAC=60°
∠BAC=60°
∴△AOM为等边三角形
 .
.
在R t △AMN中,∠AMN=30°,





考点:圆切线的证明和求不规则图形面积
点评:该题是常考题,主要考查学生对圆相关性质的理解和应用以及掌握圆切线的证明方法,不规则图形的面积通常用割补法计算。


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源:2013年浙江省鄞州八校中考模拟测试数学试卷(解析版) 题型:填空题
如图,在 中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是
中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是

查看答案和解析>>
科目:初中数学 来源:2012-2013学年浙江省宁波地区第二学期九年级模拟测试数学试卷(解析版) 题型:填空题
如图,在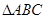 中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是
中,AB=10,AC=8,BC=6,经过点C且与边AB相切的动圆与CA,CB分别相交于点P,Q,则线段PQ长度的最小值是 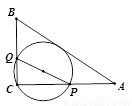
查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建省初三上学期期中考试数学试卷(解析版) 题型:解答题
如图,在 中,AB=AC,D是底边BC的中点, 作DE⊥AB于E,DF⊥AC于F求证:DE=DF.
中,AB=AC,D是底边BC的中点, 作DE⊥AB于E,DF⊥AC于F求证:DE=DF.

查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:选择题
如图,在 中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )
中,AB=AC=5,BC=6,点E,F是中线AD上的两点,则图中阴影部分的面积是( )
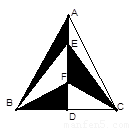
A.6 B.12 C.24 D.30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com