
【题目】如图,CD∥AB,∠ABC,∠BCD 的角平分线交 AD 于 E 点,且 E 在 AD 上,CE 交 BA 的延长线于 F 点.
(1)试问 BE 与 CF 互相垂直吗?若垂直,请说明理由;
(2)若 CD=3,AB=4,求 BC 的长 .
【答案】
(1)解:垂直,理由如下:
∵CD∥AB,
∴∠ABC+∠BCD=180°,
又∵∠ABC,∠BCD的角平分线交于E点,
∴∠ABE=∠EBC,∠DCE=∠ECB,
∴∠EBC+∠ECB=![]() ∠ABC+
∠ABC+![]() ∠BCD=
∠BCD=![]() (∠ABC+∠BCD)=90°,
(∠ABC+∠BCD)=90°,
∴∠CEB=90°,
∴BE 与 CF 互相垂直.
(2)解:由(1)知∠CEB=90°,
∴∠FEB=90°,
在△FBE 和△CBE 中,
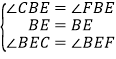
∴△FBE≌△CBE(ASA),
∴BF=BC,EF=EC,
又∵CD∥AB,
∴∠DCE=∠AFE,
在△DCE和△AFE中,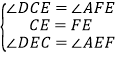
∴△DCE≌△AFE,
∴DC=AF,
∵CD=3,AB=4,
∴BC=BF=AF+AB=CD+AB=3+4=7,
【解析】(1)垂直,理由如下:由两直线平行,同旁内角互补得出∠ABC+∠BCD=180°;又由角平分线定义得出∠EBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠BCD,
∠BCD,
从而得出∠EBC+∠ECB=90°,根据三角形内角和定理得出∠CEB=90°,即BE 与 CF 互相垂直.
(2)由(1)知∠CEB=∠FEB=90°,根据ASA得△FBE≌△CBE,再由全等三角形的性质得出BF=BC,EF=EC;又由两直线平行,内错角相等,得到∠DCE=∠AFE,由ASA得△DCE≌△AFE,再根据全等三角形的性质得出DC=AF,由已知条件和等量代换求出BC的值.
【考点精析】关于本题考查的角的平分线和平行线的性质,需要了解从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.
(1)求这种笔和本子的单价;
(2)该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC∽△A1B1C1,若△ABC与△A1B1C1的相似比为3:2,则△ABC与△A1B1C1的周长之比是( )
A.2:3B.9:4C.3:2D.4:9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沭阳近年来经济快速发展,2019年GDP约达到95 000 000 000元.将95 000 000 000用科学记数法表示为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个零件的形状如图,按规定∠A= 90°,∠B、∠C 分别是 32°和 21°.某检验工人量得∠BDC= 148°,就断定这个零件不合格,试用三角形的有关知识说明零件不合格的理由.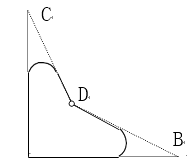
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题:“P 是等边△ABC 内的一点,若 P 到三边的距离相等,则 PA=PB=PC.”
(1)写出它的逆命题.判断其逆命题成立吗?若成立,请给出证明.
(2)进一步证明:点 P 到等边△ABC 各边的距离之和为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
为了迎接春运高峰,铁路部门日前开始调整列车运行图,2015年春运将迎来“高铁时代”.甲、乙两个城市的火车站相距1280千米,加开高铁后,从甲站到乙站的运行时间缩短了11小时,大大方便了人们出行.已知高铁行使速度是原来火车速度的3.2倍,求高铁的行驶速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级5班的李军同学为了解他家所在小区居民的用电情况,随机对该小区20户居民进行了调查,下表是这20户小区居民2015年10月份用电量的调查结果:那么关于这20户小区居民月用电量(单位:度),下列说法正确的是( )
居民(户) | 2 | 6 | 4 | 8 |
月用电量(度/户) | 40 | 50 | 55 | 60 |
A.中位数是55
B.众数是8
C.方差是29
D.平均数是53.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com