
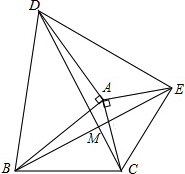
 如图,在△ABC外有△ABD和△ACE,且∠DAB=∠EAC=90°,AD=AB,AC=AE,DC交BE于M.求证:①DC=BE,②DC⊥BE,③AM平分∠DME.
如图,在△ABC外有△ABD和△ACE,且∠DAB=∠EAC=90°,AD=AB,AC=AE,DC交BE于M.求证:①DC=BE,②DC⊥BE,③AM平分∠DME. 分析 ①由等腰直角三角形的性质得到AB=AD,AE=AC,∠DAB=∠EAC=60°,然后可证明∠DAC=∠BAE,接下来证明△DAC≌△BAE可得到DC=BE;
②根据全等三角形的判定与性质,可得∠AEB与∠ACD的关系,根据三角形的内角和,可得答案.
③过点A作AF⊥DC,AG⊥BE,垂足分别为F、G.首先证明△DAF≌△BAG,依据全等三角形的性质得到AF=AG,最后依据到角两边距离相等的点在角的平分线上.
解答 解:①∵△ABD、△AEC都是等腰直角三角形,
∴AB=AD,AE=AC,∠DAB=∠EAC=60°.
∴∠DAC=∠BAE.
∵在△DAC和△BAE中$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△DAC≌△BAE(SAS).
∴DC=BE.
②∵△ABD、△AEC都是等边三角形,
∴AB=AD,AE=AC,∠DAB=∠EAC=60°.
∴∠DAC=∠BAE.
∵在△DAC和△BAE中$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△DAC≌△BAE(SAS).
∠AEB=∠ACD.
∵∠AEB+∠EAC=∠EMC+∠ACD,
∴∠EMC=∠EAC=90°,
∴DC⊥BE.
③过点A作AF⊥DC,AG⊥BE,垂足分别为F、G.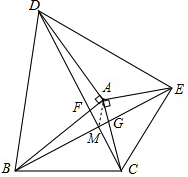
∵AF⊥DC,AG⊥BE,
∴∠DFA=∠BGA=90°.
∵△DAC≌△BAE,
∴∠ADC=∠ABE.
在△DAF和△BAG中$\left\{\begin{array}{l}{∠ADC=∠ABE}\\{∠DFA=∠BGA}\\{AD=AB}\end{array}\right.$,
∴△DAF≌△BAG.
∴AF=AG.
又∵AF⊥DC,AG⊥BE,
∴MA为∠DME的角平分线.
点评 本题主要考查全等三角形的性质和判定、角平分线的性质,掌握本题辅助线的做法是解题的关键.


 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:解答题
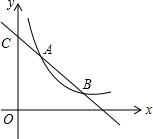 如图,直线y=kx+b与y轴相交于点C(0,8),与双曲线y=$\frac{12}{x}$相交于A(2,a),B两点,求该直线的解析式及点B的坐标.
如图,直线y=kx+b与y轴相交于点C(0,8),与双曲线y=$\frac{12}{x}$相交于A(2,a),B两点,求该直线的解析式及点B的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 m | B. | 12 m | C. | 8 m | D. | 10 m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
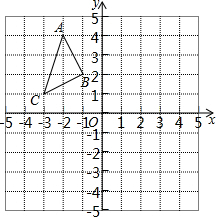 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-2,4),B(-1,2),C(-3,1),△ABC与△A1B1C1关于y轴轴对称.
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-2,4),B(-1,2),C(-3,1),△ABC与△A1B1C1关于y轴轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解全班同学的身高情况 | B. | 了解全校教师的年龄 | ||
| C. | 了解某单位的家庭收入情况 | D. | 了解全国中学生的视力情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB、CD相交于点O,AD=CB,请你补充一个条件,使得△ABD≌△CDB,你补充的条件是( )
如图,AB、CD相交于点O,AD=CB,请你补充一个条件,使得△ABD≌△CDB,你补充的条件是( )| A. | AO=CO | B. | DO=BO | C. | AB=CD | D. | ∠A=∠C |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 南偏东20° | B. | 西偏南70° | C. | 南偏东70° | D. | 西偏南20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2=1,b2=2,c2=3 | B. | b=c,∠A=45° | ||
| C. | ∠A=$\frac{3}{2}$∠B=3∠C | D. | a+b=2.5,a-b=1.6,c=2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com