
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{5}$或3 | D. | $\sqrt{5}$或$\sqrt{2}$ |
分析 由于两条线段的长分别为$\sqrt{2}$和$\sqrt{7}$,要使这个三角形是直角三角形”指代不明,因此,要讨论第三边是直角边和斜边的情形.
解答 解:当第三条线段为直角边时,$\sqrt{7}$为斜边,根据勾股定理得第三边长为$\sqrt{(\sqrt{7})^{2}-(\sqrt{2})^{2}}$=$\sqrt{5}$;
当第三条线段为斜边时,根据勾股定理得第三边长为$\sqrt{(\sqrt{7})^{2}+(\sqrt{2})^{2}}$=3.
故能与它们组成直角三角形的线段长是$\sqrt{5}$或3.
故选:C.
点评 此题主要考查了勾股定理的应用,关键是要分类讨论,不要漏解.


科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
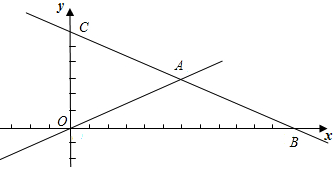
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
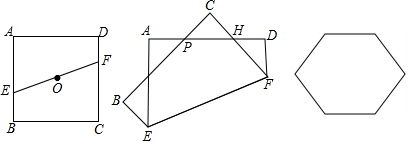
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com