
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第九卷《勾股》章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门几何步而见木( )
A.300步B.315步C.400步D.415步
科目:初中数学 来源: 题型:
【题目】包河区发展农业经济产业,在大圩乡种植多品种的葡萄.已知某葡萄种植户李大爷的葡萄成本为10元![]() ,如果在未来40天葡萄的销售单价
,如果在未来40天葡萄的销售单价![]() (元
(元![]() )与时间
)与时间![]() (天)之间的函数关系式为:
(天)之间的函数关系式为: ,且葡萄的日销售量
,且葡萄的日销售量![]() (千克)与时间
(千克)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | 40 |
日销售量 | 118 | 114 | 108 | 100 | 80 | 40 |
(1)请直接写出![]() 与
与![]() 之间的变化规律符合什么函数关系?并求在第15天的日销售量是多少千克?
之间的变化规律符合什么函数关系?并求在第15天的日销售量是多少千克?
(2)在后20天(即![]() ),请求出哪一天的日销售利润最大?日销售利润最大为多少?
),请求出哪一天的日销售利润最大?日销售利润最大为多少?
(3)在实际销售的前20天中,李大爷决定每销售1千克水果就捐赠![]() 元利润(
元利润(![]() )给留守贫困儿童作为助学金,前20天销售完后李大爷发现,每天扣除捐赠后的日销售利润随时间
)给留守贫困儿童作为助学金,前20天销售完后李大爷发现,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,请求出
的增大而增大,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
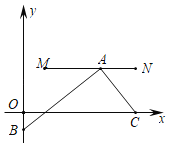
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作AB⊥AC交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
A.![]() ≤b≤1B.
≤b≤1B.![]() ≤b≤1C.
≤b≤1C.![]() ≤b≤
≤b≤![]() D.
D.![]() ≤b≤1
≤b≤1
查看答案和解析>>
科目:初中数学 来源: 题型:
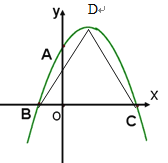
【题目】如图,二次函数![]() 图象与
图象与![]() 轴交于A、B与
轴交于A、B与![]() 轴交于C,OA=2,OB=1 ,OC=4
轴交于C,OA=2,OB=1 ,OC=4
(1).求二次函数解析式;
(2).若点D为抛物线的顶点,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
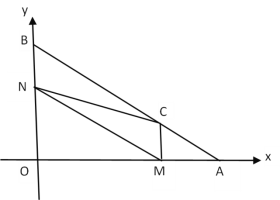
【题目】如图,在平面直角坐标系中,A (8,0) ,B (0,6),动点M从点A出发沿AO以每秒2个单位长度的速度向原点O运动,同时动点N从点B出发沿折线BO﹣OA向终点A运动,点N在y轴上的速度是每秒3个单位长度,在x轴上的速度是每秒4个单位长度,过点M作x轴的垂线交AB于点C,连结MN、CN.设点M运动的时间为t(秒),△MCN的面积为S(平方单位).
(1)当t为何值时,点M、N相遇?
(2)求△MCN的面积S(平方单位)与时间t(秒)的函数关系式;
(3)当t为何值时,△MCN是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
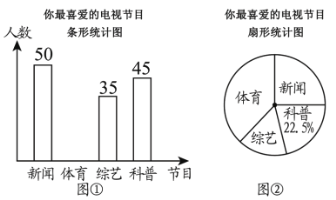
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某政府在广场上树立了如图所示的宣传牌,数学兴趣小组的同学想利用所学的知识测量宣传牌的高度AB,在D处测得点A、B的仰角分别为38°、21°,已知CD=20m,点A、B、C在一条直线上,AC⊥DC,求宣传牌的高度AB(sin21°≈0.36,cos21°≈0.93,tan21°≈0.38,sin38°≈0.62,cos38°≈0.78,tan38°≈0.79,结果精确到1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 为常数,
为常数,![]() )经过点
)经过点![]() ,点
,点![]() 是
是![]() 轴正半轴上的动点.
轴正半轴上的动点.
(Ⅰ)当![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(Ⅱ)点![]() 在抛物线上,当
在抛物线上,当![]() ,
,![]() 时,求
时,求![]() 的值;
的值;
(Ⅲ)点![]() 在抛物线上,当
在抛物线上,当![]() 的最小值为
的最小值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com