
【题目】如图,在△ABC中,∠C=90°,点O、D分别为AB、BC的中点,做⊙O与AC相切于点E,在AC边上取一点F,使DF=DO.
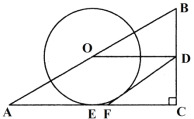
⑴求证:DF是⊙O切线;⑵若sinB=![]() ,CF=2,求⊙O的半径.
,CF=2,求⊙O的半径.
【答案】(1)证明略;(2)⊙O的半径![]() .
.
【解析】
(1)作OG⊥DF于G.连接OE.先证明△OGD≌△DCF得出OG=CD,再证明四边形CDOE是平行四边形,得出OG=OE即可解决问题;
(2)由FA,FD是⊙O的切线,推出FG=FE,设FG=FE=x,由△OGD≌△DCF(AAS),推出DG=CF=2,推出OD=DF=2+x,由AC=2OD,CE=OD,推出AE=EC=OD=2+x,由sinB=![]() 推出∠A=30°,推出
推出∠A=30°,推出![]() ,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题.
,在Rt△DCF中,根据DF2=CD2+CF2,构建方程即可解决问题.
(1)证明:作OG⊥DF于G.连接OE.
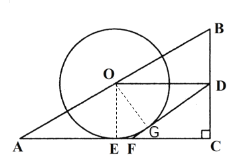
∵BD=DC,BO=OA,
∴OD∥AC,
∴∠ODG=∠DFC,
∵∠OGD=∠DCF=90°,OD=DF,
∴△OGD≌△DCF(AAS),
∴OG=CD,
∵AC是⊙O的切线,
∴OE⊥AC,
∴∠AEO=∠C=90°,
∴OE∥BC,
∵OD∥CE,
∴四边形CDOE是平行四边形,
∴CD=OE,
∴OG=OE,
∴DF是⊙O的切线.
(2)解:∵FA,FD是⊙O的切线,
∴FG=FE,设FG=FE=x,
∵△OGD≌△DCF(AAS),
∴DG=CF=2
∴OD=DF=2+x
∵AC=2OD,CE=OD,
∴AE=EC=OD=2+x
∵sinB=![]() .
.
∴∠B=60°,
∴∠A=30°,
![]()
在Rt△DCF中,∵DF2=CD2+CF2,
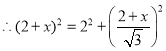
解得![]() 或
或![]()
![]()
即⊙O的半径是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
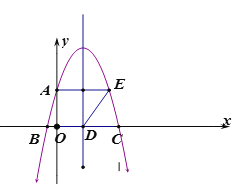
【题目】已知:如图抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈市某中学为了丰富校园文化生活.校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查。将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
(1)通过计算补全条形统计图;
(2)在这次调查中,一共抽取了多少名学生?
(3)如果全校有680名学生,请你估计这680名学生中参加演讲比赛的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=2,BC=5,点I为△ABC的内心,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为( )
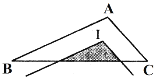
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海上有A、B、C三座小岛,小岛B在岛A的正北方向,距离为121海里,小岛C分别位于岛B的南偏东53°方向,位于岛A的北偏东27°方向,求小岛B和小岛C之间的距离.(参考数据:sin27°≈![]() ,cos27°≈
,cos27°≈![]() ,tan27°≈
,tan27°≈![]() ,sin53°≈
,sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
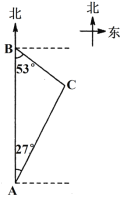
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为![]() 的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为
的空地进行绿化,一部分种草,剩余部分栽花.设种草部分的面积为![]() ,种草所需费用
,种草所需费用![]() (元)与
(元)与![]() 的函数关系式为
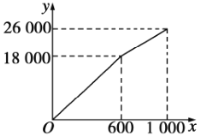
的函数关系式为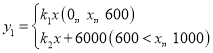 ,其大致图象如图所示.栽花所需费用
,其大致图象如图所示.栽花所需费用![]() (元)与
(元)与![]() 的函数关系式为
的函数关系式为![]() .
.
(1)求出![]() ,
,![]() 的值;
的值;
(2)若种花面积不小于![]() 时的绿化总费用为
时的绿化总费用为![]() (元),写出
(元),写出![]() 与
与![]() 的函数关系式,并求出绿化总费用
的函数关系式,并求出绿化总费用![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
(1)求点![]() 的坐标.
的坐标.
(2)当![]() 时,经过点
时,经过点![]() 的直线
的直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() .该抛物线在直线
.该抛物线在直线![]() 上方的部分与线段
上方的部分与线段![]() 组成一个新函数的图象.请结合图象回答:若新函数的最小值大于
组成一个新函数的图象.请结合图象回答:若新函数的最小值大于![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
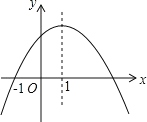
【题目】如图是二次函数![]() 的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(
的图象,其对称轴为x=1,下列结论:①abc>0;②2a+b=0;③4a+2b+c<0;④若(![]() ,y1),(
,y1),(![]() ,y2)是抛物线上两点,则y1<y2,其中正确的结论有( )个
,y2)是抛物线上两点,则y1<y2,其中正确的结论有( )个
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织七、八、九年级学生参加“州庆60年,梦想红河”作文比赛.该校将收到的参赛作文进行分年级统计,绘制了如图1和图2两幅不完整的统计图. 根据图中提供的信息完成以下问题.
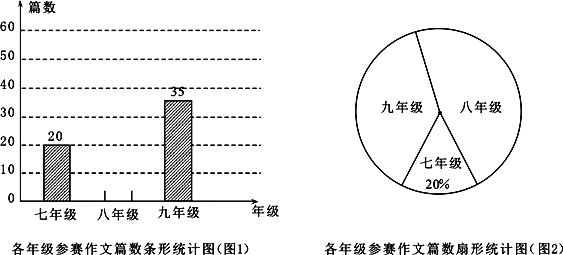
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(2)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,把七年级特等奖作文被选登在校刊上的事件记为A,其它年级特等奖作文被选登在校刊上的事件分别记为B,C,D. 请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com