
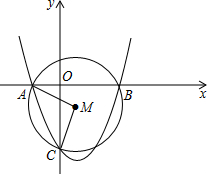
 如图,二次函数y=x2-2x-3的图象经过(a,0),B(b,0),C(0,c)三点,(a<b)
如图,二次函数y=x2-2x-3的图象经过(a,0),B(b,0),C(0,c)三点,(a<b)分析 (1)根据坐标轴上点的坐标特征,解方程求出a、b、c的值;
(2)作ME⊥AB于E,MF⊥CD于F,根据相交弦定理求出OD,根据勾股定理和扇形面积公式计算即可.
解答 解: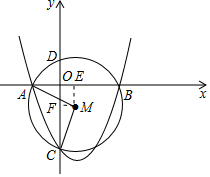 (1)当y=0时,x2-2x-3=0,
(1)当y=0时,x2-2x-3=0,
x1=-1,x2=3,
当x=0时,y=-3,
则a=-1、b=3、c=3;
(2)作ME⊥AB于E,MF⊥CD于F,
由(1)得,OA=1,OB=3,OC=3,
∵OA•OB=OC•OD,
∴OD=1,
∴OE=OF=1,
∴MA=MC=$\sqrt{5}$,
∵OA=1,OC=3,
∴AC=$\sqrt{10}$,
∴△AMC为等腰直角三角形,即∠AMC=90°,
则半径MA、MC及劣弧AC围成的扇形的面积为:$\frac{90π×(\sqrt{5})^{2}}{360}$=$\frac{25π}{4}$.
点评 本题考查的是二次函数图象上点的坐标特征、扇形面积的计算,掌握坐标轴上点的坐标特征、扇形面积公式是解题的关键.


 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 .
.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
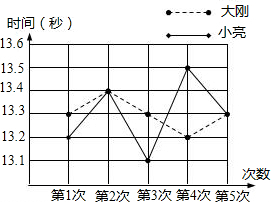
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 大刚 | 13.3 | 13.4 | 13.3 | 13.2 | 13.3 |
| 小亮 | 13.2 | 13.4 | 13.1 | 13.5 | 13.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com