
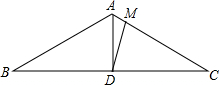
 如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,M为AC上一点,且CM=CD,则∠ADM=15°.
如图,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,M为AC上一点,且CM=CD,则∠ADM=15°. 分析 先根据等腰三角形两底角相等求出∠C,再根据CM=CD即可求出∠CDM的度数,再根据等腰三角形三线合一的性质求出∠ADC=90°,∠ADM即可求出.
解答 解:在△ABC中,AB=AC,∠BAC=120°,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
又∵CM=CD,
∴∠CDM=∠CMD=$\frac{1}{2}$×(180°-30°)=75°,
∵AB=AC,BD=CD,
∴AD⊥BC,即∠ADC=90°,
∴∠ADM=∠ADC-∠CDM=90°-75°=15°.
故答案为:15.
点评 此题考查等腰三角形的基本性质;充分利用等腰三角形三线合一的性质和等边对等角性质来求解是解题的关键.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是$\frac{27}{2}$,S3的值为$\frac{{3}^{8}}{{2}^{5}}$.
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是$\frac{27}{2}$,S3的值为$\frac{{3}^{8}}{{2}^{5}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD各顶点的坐标分别为A(2,6),B(4,2),C(6,2),D(6,4),在第一象限内,画出以原点为位似中心,与原四边形ABCD相似比为$\frac{1}{2}$的位似图形A1B1C1D1,并写出各点坐标.
如图,四边形ABCD各顶点的坐标分别为A(2,6),B(4,2),C(6,2),D(6,4),在第一象限内,画出以原点为位似中心,与原四边形ABCD相似比为$\frac{1}{2}$的位似图形A1B1C1D1,并写出各点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com