
【题目】如图,若△A1B1C1是由△ABC平移后得到的,且△ABC中任意一点P(x,y)经过平移后的对应点为P1(x﹣5,y+2).
(1)在下图方格中画出△A1B1C1.
(2)求点A1、B1、C1的坐标.
(3)求△A1B1C1的面积.
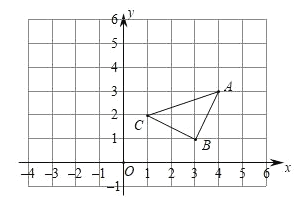
【答案】(1)答案见解析;(2)点A1的坐标为(-1,5),点B1的坐标为(-2,3),点C1的坐标为(-4,4);(3)△A1B1C1的面积为2.5.
【解析】
(1)、由题意得△A1B1C1是由△ABC向左平移5个单位长度,向上平移2个单位长度后得到的,所以找到A、B、C点的对应点再连接即可;
(2)、将A、B、C三点的横坐标减5,纵坐标减2后得到的对应点即为A1、B1、C1的坐标;
(3)、利用割补法,结合不规则三角形构造一个规则图形求面积即可.
(1)由题意得:△A1B1C1是由△ABC向左平移5个单位长度,向上平移2个单位长度后得到的,所以找到A、B、C点的对应点再连接,如下图所示:

(2)点A1的坐标为(-1,5),点B1的坐标为(-2,3),点C1的坐标为(-4,4);
(3)如下图利用割补法,将不规则的△A1B1C1补全为一个直角梯形,则:
△A1B1C1的面积=直角梯形A1EDC1的面积-△A1B1E的面积-△B1C1D的面积
△A1B1C1的面积=![]()



科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,点D为△ABC外一点,DC与AB交于点O,且∠BDC=∠BAC.
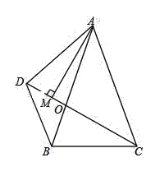
(1)求证:∠ABD=∠ACD;
(2)过点A作AM⊥CD于M,求证:BD+DM=CM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,点D在线段AB上.
(1)如图1,若AB=12,BD=![]() BC,求线段CD的长度;
BC,求线段CD的长度;
![]()
(2)如图2,点E是线段AB上一点,且AE=2BE,当3AD=2BD时,探究线段CD与CE之间的数量关系,请说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
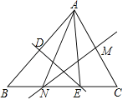
【题目】如图,△ABC中,∠BAC=80°,BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,NE=6,则∠NAE=______°,△EAN的周长=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC的平分线,分别交AD,AC于P,Q两点,并证明AP=AQ.(要求:尺规作图,保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点A表示数1,现将点A沿数轴做如下移动:第一次将点A向左移动3个单位长度到达点![]() ,第2次将点
,第2次将点![]() 向右平移6个单位长度到达点
向右平移6个单位长度到达点![]() ,第3次将点
,第3次将点![]() 向左移动9个单位长度到达点
向左移动9个单位长度到达点![]() …,按照这种规律移动下去,则第2017次移动到点
…,按照这种规律移动下去,则第2017次移动到点![]() 时,
时,![]() 在数轴上对应的实数是_______.
在数轴上对应的实数是_______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知D,E分别为边BC,AD的中点,且S△ABC=4 cm2,则△BEC的面积为( )

A. 2 cm2 B. 1 cm2 C. 0.5 cm2 D. 0.25 cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com