练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．计算：$\sqrt{2}$+$\frac{1}{\sqrt{8}}$=$\frac{5\sqrt{2}}{4}$．

    分析 原式第二项化简后，合并即可得到结果．

    解答 解：原式=$\sqrt{2}$+$\frac{\sqrt{2}}{4}$=$\frac{5\sqrt{2}}{4}$，
    故答案为：$\frac{5\sqrt{2}}{4}$

    点评 此题考查了二次根式的加减法，以及分母有理化，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    9．如图，已知△ABC中，DE∥BC，连接BE，△ADE的面积是△BDE面积的$\frac{1}{2}$，则S△ADE：S△ABC=1：9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

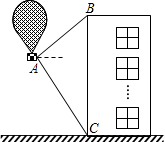    10．“五一”节期间在我市市民广场进行了热气球飞行表演，如图，有一热气球到达离地面高度为36米的A处时，仪器显示如图，有一热气球到达离地面高度为36米的A处时，仪器显正前方一高楼顶部B的仰角是37°，底部C的俯角是60°．为了安全飞越高楼，气球应至少再上升多少米？（结果精确到0.1米）
    （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．若等腰三角形的一个外角的度数为40°，则这个等腰三角形顶角的度数是140°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

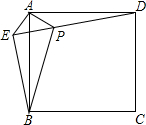    14．如图，点E是正方形ABCD外一点，连接AE，BE和DE，过点A作AE的垂线交DE于P，若AE=AP=1，PB=3，下列结论：
    ①△ADP≌△ABE；
    ②BE⊥DE；
    ③点B到直线AE的距离为$\sqrt{7}$；
    ④S正方形ABCD=8+$\sqrt{14}$，
    其中正确结论的序号是①，②，④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图，四边形ABCD、AEFG是正方形，点E、G分别在AB、AD上，连接FC，过点E作EH∥FC，交BC于点H，若AB=4，AE=1，则BH=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，某一时刻太阳光从教室窗户射入室内，与地面的夹角∠BPC为30°，窗户的一部分在教室地面所形成的影长PE为3.5米，窗户的高度AF为2.5米．求窗外遮阳蓬外端一点D到教室窗户上椽的距离AD．（参考数据：$\sqrt{3}$≈1.7，结果精确0.1米）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．甲地到乙地之间的铁路长210千米，动车运行后的平均速度是原来火车的1.8倍，这样由甲地到乙地的行驶时间缩短了1.5小时，设原来火车的平均速度为x千米/小时，则下列方程正确的是（　　）
    A．$\frac{210}{x}$-1.8=$\frac{210}{1.5x}$B．$\frac{210}{x}$+1.8=$\frac{210}{1.5x}$
    C．$\frac{210}{x}$+1.5=$\frac{210}{1.8x}$D．$\frac{210}{x}$-1.5=$\frac{210}{1.8x}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

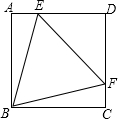    9．如图，正方形ABCD中，点E、F分别在AD、DC上，且△BEF为等边三角形．下列结论：①DE=DF；②∠AEB=75°；③AE+CF=EF；④BE=$\sqrt{2}$DE；⑤△EDF与△BFC的面积比为2：1．其中正确的结论有4个．

    查看答案和解析>>

    同步练习册答案