
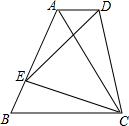
 如图,四边形ABCD中,AD∥BC,AD<BC,AB=AC,点E在AB上,连接DE、DC、EC,∠DCE=∠ACB.
如图,四边形ABCD中,AD∥BC,AD<BC,AB=AC,点E在AB上,连接DE、DC、EC,∠DCE=∠ACB.分析 (1)先根据AD∥BC得出∠DAC=∠ACB,再由AB=AC可得出∠ABC=∠ACB,故可得出∠DAC=∠ABC,根据∠DCE=∠ACB可得出∠ACD=∠BCE,据此可得出结论;
(2)先根据平行线的性质得出∠BAD+∠ABC=180°,再由∠DCE=∠ACB可知∠DCE+∠BAD=180°,故A、E、C、D四点共圆,故可得出∠DEC=∠DAC,再由∠DAC=∠DCE可得出∠DCE=∠DEC,故DE=DC.
解答 (1)证明:∵AD∥BC,
∴∠DAC=∠ACB.
∵AB=AC,
∴∠ABC=∠ACB,
∴∠DAC=∠ABC.
∵∠DCE=∠ACB,
∴∠ACD=∠BCE,
∴△ACD∽△BCE;
(2)证明:∵AD∥BC,
∴∠BAD+∠ABC=180°.
∵∠DCE=∠ACB,
∴∠DCE+∠BAD=180°,
∴A、E、C、D四点共圆,
∴∠DEC=∠DAC.
∵∠DAC=∠DCE,
∴∠DCE=∠DEC,
∴DE=DC.
点评 本题考查的是相似三角形的判定与性质,涉及到平行线的性质、相似三角形的判定及四点共圆的相关知识,难度适中.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 红星中学为了解七年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
红星中学为了解七年级学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:| 发言次数n | |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知正方形A1B1C1D1的面积为1,把它的各边延长一倍得到新的正方形A2B2C2D2,再将正方形A2B2C2D2各边长延长一倍得到正方形A3B3C3D3,以此下去…,则正方形A9B9C9D9的周长是2500.
如图,已知正方形A1B1C1D1的面积为1,把它的各边延长一倍得到新的正方形A2B2C2D2,再将正方形A2B2C2D2各边长延长一倍得到正方形A3B3C3D3,以此下去…,则正方形A9B9C9D9的周长是2500.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com