
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
分析 根据反比例函数的性质可得出关于m的一元一次不等式,解不等式可得出m的取值范围,再根据根的判别式△=9-8m即可得出△的取值范围,由此即可得出结论.
解答 解:∵函数y=$\frac{m+2}{x}$的图象在第二、四象限,
∴m+2<0,
解得:m<-2.
在方程mx2-3x+2=0中,△=(-3)2-4m×2=9-8m,
∵m<-2,
∴△=9-8m>25>0,
∴方程mx2-3x+2=0有两个不相等的实数根.
故选A.
点评 本题考查了根的判别式意义反比例函数的性质,解题的关键是找出△=9-8m>25.本题属于基础题,难度不大,解决该题型题目时,根据根的判别式的正负得出方程根的个数是关键.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
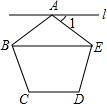 (1)计算:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1
(1)计算:(2-π)0-$\sqrt{8}$×$\sqrt{2}$+($\frac{1}{3}$)-1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
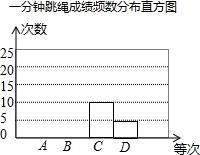 为备战体育中考,李明同学就自己平时1分钟跳绳的训练成绩,做了认真统计,并将训练成绩绘出了如下的频数分布表和频数分布直方图(不完整).(规定:1分钟跳绳120个以下成绩为D等;120-140个为C等;140-160个为B等;160个以上为A等)
为备战体育中考,李明同学就自己平时1分钟跳绳的训练成绩,做了认真统计,并将训练成绩绘出了如下的频数分布表和频数分布直方图(不完整).(规定:1分钟跳绳120个以下成绩为D等;120-140个为C等;140-160个为B等;160个以上为A等)| 成绩等次 | 频数(人) | 频率 |
| D | 5 | 0.1 |
| C | 10 | 0.2 |
| B | 25 | 0.5 |
| A | 10 | 0.2 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 流量阶梯定价标准 | |
| 使用范围 | 阶梯单价(元/MB) |
| 1-100MB | a |
| 101-500MB | 0.07 |
| 501MB-20GB | b |
| 语音阶梯定价标准 | |
| 使用范围 | 阶梯资费(元/分钟) |
| 1-500分钟 | 0.15 |
| 501-1000分钟 | 0.12 |
| 1001-2000分钟 | m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9)阴影三角形部分的面积从左向右依次为S1、S2、S3…Sn,则第4个正方形的边长是$\frac{27}{2}$Sn的值为$\frac{{3}^{4n-4}}{{2}^{4n-7}}$
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9)阴影三角形部分的面积从左向右依次为S1、S2、S3…Sn,则第4个正方形的边长是$\frac{27}{2}$Sn的值为$\frac{{3}^{4n-4}}{{2}^{4n-7}}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com