
 在平面直角坐标系中,长方形ABCD的边BC∥x轴,如图所示,若A点坐标为(-1,2$\sqrt{2}$),C点坐标为(3,-2$\sqrt{2}$)
在平面直角坐标系中,长方形ABCD的边BC∥x轴,如图所示,若A点坐标为(-1,2$\sqrt{2}$),C点坐标为(3,-2$\sqrt{2}$)分析 (1)根据A、D点的坐标,点A与点B关于x轴对称,点C与点D关于x轴对称,可得答案;
(2)①当P点运动时间1秒时,P点在AD上,△BCP的面积=$\frac{1}{2}$BC•AB;
②当P点 运动时间4秒时,P点在DC上,△BCP的面积=$\frac{1}{2}$BC•CP;
③当P点运动时间6秒时,P点在DC上,△BCP的面积=$\frac{1}{2}$BC•CP.
解答 解:(1)根据题意可知,点A与点B关于x轴对称,点C与点D关于x轴对称,
∴点B的坐标是(-1,-2$\sqrt{2}$),点D的坐标是(3,2$\sqrt{2}$);
(2)根据题意得:AB=CD=2$\sqrt{2}$+2$\sqrt{2}$=4$\sqrt{2}$,AD=BC=1+3=4,
①当P点运动时间1秒时,AP=$\sqrt{2}$<AD,
∴P点在AD上,
∴△BCP的面积=$\frac{1}{2}$BC•AB=$\frac{1}{2}$×4×4$\sqrt{2}$=8$\sqrt{2}$≈11.3;
②当P点 运动时间4秒时,P点运动了4$\sqrt{2}$,
∵AD<4$\sqrt{2}$<AD+DC,
∴P点在DC上,CP=4$\sqrt{2}$-(4$\sqrt{2}$-4)=4,
∴△BCP的面积=$\frac{1}{2}$BC•CP=$\frac{1}{2}$×4×4=8;
③当P点运动时间6秒时,P点运动了6$\sqrt{2}$,
∵AD<6$\sqrt{2}$<AD+DC,
∴P点在DC上,CP=4$\sqrt{2}$-(6$\sqrt{2}$-4)=4-2$\sqrt{2}$,
∴△BCP的面积=$\frac{1}{2}$BC•CP=$\frac{1}{2}$×4×(4-2$\sqrt{2}$)=8-4$\sqrt{2}$≈2.3.
点评 本题是四边形综合题目,考查了坐标与图形性质、轴对称的性质、矩形的性质、三角形的面积计算等知识;本题综合性强,熟练掌握坐标与图形性质是解决问题的关键.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
| A. | m≥3 | B. | m≤3 | C. | m=3 | D. | m<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
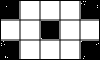 一只小狗跳来跳去,然后随意落在如图所示的某一方格中(每个方格除颜色外完全相同),则小狗停留在黑色方格中的概率是$\frac{1}{3}$.
一只小狗跳来跳去,然后随意落在如图所示的某一方格中(每个方格除颜色外完全相同),则小狗停留在黑色方格中的概率是$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的对角线相交于O,过点O作OE⊥BD,交AD点E,连接BE,若∠ABE=20°,则∠AOE的大小是( )
如图,矩形ABCD的对角线相交于O,过点O作OE⊥BD,交AD点E,连接BE,若∠ABE=20°,则∠AOE的大小是( )| A. | 10° | B. | 15° | C. | 20° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
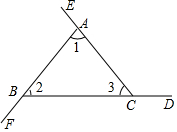 用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com