练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：如图，将矩形ABCD沿着直线BD折叠，使点C落在C1处，BC1交AD于E，AD＝8，AB＝4，求△BED的面积．

    答案：
    解析：

    　　解：在矩形ABCD中，AD∥BC，∴∠2＝∠3，

    　　当矩形ABCD沿直线BD折叠后，△BC1D与△BCD关于直线BD对称，

    　　∴∠1＝∠2，(注意折叠中的不定量)

    　　∴∠1＝∠3，故BE＝DE．

    　　做EF⊥BD于F，则BF＝BD，BD＝＝4．

    　　(等腰三角形“三线合一”的性质)

    　　设BE＝x，∵BE＝DE，∴AE＝8－x，

    　　在Rt△ABE中，42＋(8－x)2＝x2，∴x＝5．

    　　在Rt△BEF中，x2＝EF2＋(2)2，∴EF＝，

    　　∴S△BED＝BD·EF＝10．

    　　分析：求三角形面积，关键要求出底和高的大小．


    提示：

    注：本题是矩形折叠的问题，易错点是对△BED是等腰三角形的认识不足，解题关键是对折叠后的几何形状要有正确的分析．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

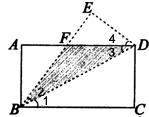    7、已知：如图，将矩形ABCD沿对角线BD翻折，点C落到点E的位置，BE交AD于F．求证：重叠部分（即△BDF）是等腰三角形．
    证明：∵四边形ABCD是矩形
    ∴AD∥BC．
    ∴--
    又∵△BDE与△BDC关于BD对称
    ∴--
    ∴∠2=∠3
    ∴△BDF是等腰三角形．
    请仔细思考：以上证明过程中，划线部分正确的应该依次是以下四项中的哪两项（　　）
    ①∠1=∠2；②∠1=∠3；③∠3=∠4；④∠BDC=∠BDE

    查看答案和解析>>

    科目：初中数学 来源：新课标3维同步训练与评价·数学·九年级·上 题型：047

    已知：如图，将矩形纸片ABCD沿对角线AC折叠，使点B落在点E处．求证：EF＝DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

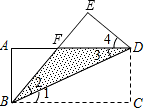    已知：如图，将矩形ABCD沿对角线BD翻折，点C落到点E的位置，BE交AD于F．求证：重叠部分（即△BDF）是等腰三角形．
    证明：∵四边形ABCD是矩形
    ∴AD∥BC．
    ∴--
    又∵△BDE与△BDC关于BD对称
    ∴--
    ∴∠2=∠3
    ∴△BDF是等腰三角形．
    请仔细思考：以上证明过程中，划线部分正确的应该依次是以下四项中的哪两项
    ①∠1=∠2；②∠1=∠3；③∠3=∠4；④∠BDC=∠BDE．


    1. A.
      ①③
    2. B.
      ②③
    3. C.
      ②①
    4. D.
      ③④

    查看答案和解析>>

    科目：初中数学 来源：2006年四川省达州市中考数学试卷（解析版） 题型：选择题

    （2006•达州）已知：如图，将矩形ABCD沿对角线BD翻折，点C落到点E的位置，BE交AD于F．求证：重叠部分（即△BDF）是等腰三角形．
    证明：∵四边形ABCD是矩形
    ∴AD∥BC．
    ∴--
    又∵△BDE与△BDC关于BD对称
    ∴--
    ∴∠2=∠3
    ∴△BDF是等腰三角形．
    请仔细思考：以上证明过程中，划线部分正确的应该依次是以下四项中的哪两项（ ）
    ①∠1=∠2；②∠1=∠3；③∠3=∠4；④∠BDC=∠BDE．

    A．①③
    B．②③
    C．②①
    D．③④

    查看答案和解析>>

    同步练习册答案