
【题目】如图,△ABC为等边三角形,O为BC的中点,作⊙O与AC相切于点D.
(1)求证:AB与⊙O相切;
(2)延长AC到E,使得CE=AC,连接BE交⊙O与点F、M,若AB=4,求FM的长.

【答案】(1)见解析;(2)2![]()
【解析】
(1)连接OD,作OG⊥AB于G,由等边三角形的性质得出∠OCD=∠OBG=∠ABC=60°,由切线的性质得出∠ODC=90°=∠OGB,证明△OBG≌△OCD得出OG=OD,即可得出结论;
(2)连接OA、OM,作OH⊥FM于H,由垂径定理得出FH=MH,证明四边形OHBG是矩形,得出OH=BG,由直角三角形的性质得出OH=BG=![]() OB=1,OG=
OB=1,OG=![]() BG=
BG=![]() ,在Rt△OMH中,由勾股定理得出MH=
,在Rt△OMH中,由勾股定理得出MH=![]() =
=![]() ,即可得出结果.
,即可得出结果.
(1)证明:连接OD,作OG⊥AB于G,如图1所示:

则∠OGB=90°,
∵△ABC为等边三角形,
∴∠OCD=∠OBG=∠ABC=60°,
∵O为BC的中点,
∴OB=OC,
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ODC=90°=∠OGB,
在△OBG和△OCD中,
 ,
,
∴△OBG≌△OCD(AAS),
∴OG=OD,
∴AB与⊙O相切;
(2)解:连接OA、OM,作OH⊥FM于H,如图2所示:

则∠OHB=90°,FH=MH,
∵CE=AC,AC=BC,
∴CE=BC,
∴∠CBE=∠CEB=![]() ∠ACB=30°,
∠ACB=30°,
∴∠ABE=∠ABC+∠CBE=90°,
∵∠OGB=90°,
∴四边形OHBG是矩形,
∴OH=BG,
∵△ABC是等边三角形,O为BC的中点,
∴OB=![]() BC=
BC=![]() AB=2,
AB=2,
∵∠BOG=90°﹣60°=30°,
∴OH=BG=![]() OB=1,OG=
OB=1,OG=![]() BG=
BG=![]() ,
,
在Rt△OMH中,OM=OG=![]() ,OH=1,
,OH=1,
∴MH=![]() =
=![]() ,
,
∴FM=2MH=2![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】在平面上,对于给定的线段AB和点C,若平面上的点P(可以与点C重合)满足,∠APB=∠ACB.则称点P为点C关于直线AB的联络点.

在平面直角坐标系xOy中,已知点A(2,0),B(0,2),C(﹣2,0).
(1)在P1(2,2),P(1,0),R(1+![]() ,1)三个点中,是点O关于线段AB的联络点的是 .
,1)三个点中,是点O关于线段AB的联络点的是 .
(2)若点P既是点O关于线段AB的联络点,同时又是点B关于线段OA的联络点,求点P的横坐标m的取值范围;
(3)直线y=x+b(b>0)与x轴,y轴分交于点M,N,若在线段BC上存在点N关于线段OM的联络点,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC与等腰三角形△EDC有公共顶点C,其中∠EDC=120°,AB=CE=2![]() ,连接BE,P为BE的中点,连接PD、AD
,连接BE,P为BE的中点,连接PD、AD
(1)为了研究线段AD与PD的数量关系,将图1中的△EDC绕点C旋转一个适当的角度,使CE与CA重合,如图2,请直接写出AD与PD的数量关系;
(2)如图1,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)如图3,若∠ACD=45°,求△ACD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,一次函数y=x﹣1的图象与x轴,y轴分别交于点A,B,与反比例函数y=![]() 的图象交于点C,D,CE⊥x轴于点E,
的图象交于点C,D,CE⊥x轴于点E,![]() .
.
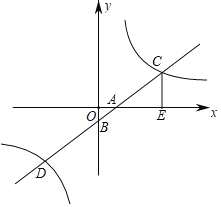
(1)求反比例函数的表达式与点D的坐标;
(2)以CE为边作ECMN,点M在一次函数y=x﹣1的图象上,设点M的横坐标为a,当边MN与反比例函数y=![]() 的图象有公共点时,求a的取值范围.
的图象有公共点时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD.已知BC=BD,AB=4.
(1)若BC=2![]() ,求证:BD是⊙O的切线;
,求证:BD是⊙O的切线;
(2)BC=3,求CD的长.
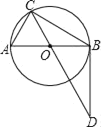
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com