
【题目】如图,在Rt△ABC中,∠ABC=90°∠ACB=60°.将Rt△ABC绕点C顺时针方向旋转后得到△DEC(△DEC≌△ABC),点E在AC上,再将Rt△ABC沿着AB所在直线翻转180°得到△ABF,连接AD.

(1)求证:四边形AFCD是菱形;
(2)连接BE并延长交AD于点G,连接CG.请问:四边形ABCG是什么特殊平行四边形?为什么?
【答案】(1)见解析;(2))四边形 ABCG 是矩形,见解析.
【解析】
(1)需证明△ACD是等边三角形、△AFC是等边三角形,即可证明四边形AFCD是菱形.(2)先证明四边形ABCG是平行四边形,再由∠ABC=90°,可证四边形ABCG是矩形。
解:(1) 证明:△DEC 是由 Rt△ABC 绕 C 点旋转后得到.
∴AC=DC,∠ACD=∠ACB=60°.
∴△ACD 是等边三角形,
∴AD=DC=AC.
又∵Rt△ABF 是由 Rt△ABC 沿 AB 所在直线翻转 180°得到
∴AC=AF,∠ABF=∠ABC=90°.
∴∠FBC 是平角,∴ 点 F、B、C 三点共线
∴△AFC 是等边三角形
∴AF=FC=AC.
∴AD=DC=FC=AF.
∴四边形 AFCD 是菱形,
(2)四边形 ABCG 是矩形.
证明:由(1)可知:△ACD 是等边三角形,∠DEC=∠ABC=90°.
∴DE⊥AC 于 E.∴AE=EC.
∵四边形 AFCD 是菱形,∴AG∥BC.
∴∠EAG=∠ECB,∠AGE=∠EBC.
∴△AEG≌△CEB,∴BE=EG.
∴四边形 ABCG 是平行四边形.
而∠ACB=90°,∴四边形 ABCG 是矩形.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
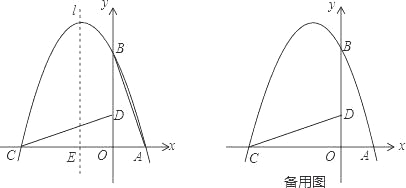
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距64 km,甲从A地出发,每小时行14 km,乙从B地出发,每小时行18 km.
(1)若两人同时出发相向而行,则需经过几小时两人相遇?
(2)若两人同时出发相向而行,则需经过几小时两人相距16 km?
(3)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“创卫工作人人参与,环境卫生人人受益”,我区创卫工作已进入攻坚阶段.某校拟整修学校食堂,现需购买A、B两种型号的防滑地砖共60块,已知A型号地砖每块80元,B型号地砖每块40元.
(1)若采购地砖的费用不超过3200元,那么,最多能购买A型号地砖多少块?
(2)某地砖供应商为了支持创卫工作,现将A、B两种型号的地砖单价都降低a%,这样,该校花费了2560元就购得所需地砖,其中A型号地砖a块,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式变形不一定正确的是( ).
A.若 x=y,则 x-5=y-5B.若 x=y,则 ax=ay
C.若 x=y,则 3-2x=3-2yD.若 x=y,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com