
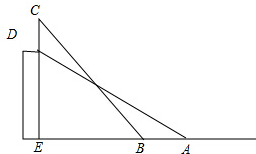
 如图所示,某高校的教学大楼上竖有一根避雷针CD,小明为了知道避雷针CD的长度,在点A测得点D的仰角为30°,小明向大楼方向行进16m到达点B,又测得点C的仰角为45°,若大楼DE高度为24m,求避雷针CD的长度(结果保留根号).
如图所示,某高校的教学大楼上竖有一根避雷针CD,小明为了知道避雷针CD的长度,在点A测得点D的仰角为30°,小明向大楼方向行进16m到达点B,又测得点C的仰角为45°,若大楼DE高度为24m,求避雷针CD的长度(结果保留根号). 分析 根据三角函数的定义得到AE=$\frac{3DE}{\sqrt{3}}$=24$\sqrt{3}$m,于是得到BE=AE-AB=(24$\sqrt{3}$-16)m,根据三角函数的定义得到CE=BE=(24$\sqrt{3}$-16)m,于是得到结论.
解答 解:由题意得DE=24m,AB=16m,∠A=30°,∠CBE=45°,
在Rt△ADE中,tan∠A=tan30°=$\frac{\sqrt{3}}{3}$=$\frac{DE}{AE}$,
∴AE=$\frac{3DE}{\sqrt{3}}$=24$\sqrt{3}$m,
∴BE=AE-AB=(24$\sqrt{3}$-16)m,
∵tan∠CBE=tan45°=1=$\frac{CE}{BE}$,
∴CE=BE=(24$\sqrt{3}$-16)m,
∴CD=CE-DE=24$\sqrt{3}$-16-24=(24$\sqrt{3}$-40)m.
答:避雷针CD的长度(2$\sqrt{3}$-40)m.
点评 本题考查了解直角三角形的应用,利用锐角三角函数的知识求出线段CE和DE的长,从而根据CD=CE-DE得出问题的答案是解决本题的关键.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com