
【题目】如图,O为菱形ABCD对角线的交点,DE∥AC,CE∥BD. 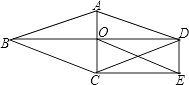
(1)试判断四边形OCED的形状,并说明理由;
(2)若AC=6,BD=8,求线段OE的长.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°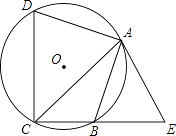
(1)求证:AE是⊙O的切线;
(2)若 AB=AD,AC=2 ![]() ,tan∠ADC=3,求CD的长.
,tan∠ADC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD,E为平面内任意一点,连结DE,将线段DE绕点D顺时针旋转90°得到DG,连结EC,AG.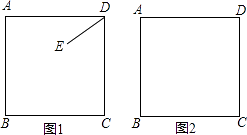
(1)当点E在正方形ABCD内部时,
①依题意补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG= ![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某公园一块草坪上的自动旋转喷水装置,这种旋转喷水装置的旋转角度为240°,它的喷灌区是一个扇形.小涛同学想了解这种装置能够喷灌的草坪面积,他测量出了相关数据,并画出了示意图.如图2,A,B两点的距离为18米,求这种装置能够喷灌的草坪面积. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(0,4),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′是直线y= ![]() x上一点,则点B与其对应点B′间的距离为 .
x上一点,则点B与其对应点B′间的距离为 . 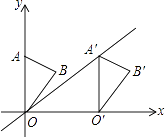
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y= ![]() 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.3
B.﹣3
C.6
D.﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1= ![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2). 
(1)求这两个函数的表达式;
(2)观察图象,直接写出y1>y2时自变量x的取值范围.
(3)连接OA、OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湿地景区岸边有三个观景台A、B、C,已知AB=1400米,AC=1000米,B点位于A点的南偏西60.7°方向,C点位于A点的南偏东66.1°方向.
(1)求△ABC的面积;
(2)景区规划在线段BC的中点D处修建一个湖心亭,并修建观景栈道AD,试求A、D间的距离.(结果精确到0.1米)
(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin60.7°≈0.87,cos60.7°≈0.49,sin66.1°≈0.91,cos66.1°≈0.41, ![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC. 
(1)求证:直线BF是⊙O的切线.
(2)若CD=2 ![]() ,OP=1,求线段BF的长.
,OP=1,求线段BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com