
【题目】如图,点A在直线l上,点B在直线l外,点B关于直线l的对称点为C,连接AC,过点B作BD⊥AC于点D,延长BD至E使BE=AB,连接AE并延长与BC的延长线交于点F.

(1)补全图形;
(2)若∠BAC=2α,求出∠AEB的大小(用含α的式子表示);
(3)用等式表示线段EF与BC的数量关系,并证明.
【答案】(1)见解析;(2)∠AEB=![]() ;(3)BC=
;(3)BC=![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据题意作图即可补全图形;
(2)先根据直角三角形两锐角互余的性质求出∠ABD,再由BE=AB,可得∠AEB=∠BAE,然后利用三角形的内角和定理即可求得结果;
(3)设l与BC交于点H,过点E作EG⊥BF于点G,如图3,先利用轴对称的性推出∠BAH=∠CAH=α,再根据质余角的性质推出∠CBD=∠CAH=α,进一步利用(2)的结论和三角形的外角性质推出∠F=45°,进而可得![]() ,然后根据AAS可证明△ABH≌△BEG,从而得BH=EG,而BC=2BH,进一步即可得出EF与BC的数量关系.
,然后根据AAS可证明△ABH≌△BEG,从而得BH=EG,而BC=2BH,进一步即可得出EF与BC的数量关系.
解:(1)补全图形如图1所示:
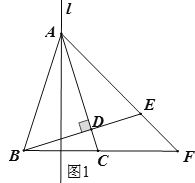
(2)∵BD⊥AC,∠BAD=2α,∴∠ABD=90°-2α,
∵BE=AB,∴∠AEB=∠BAE=![]() ;
;
(3)线段EF与BC的数量关系是:BC=![]() .
.
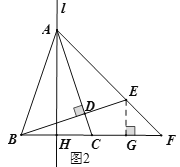
证明:设l与BC交于点H,过点E作EG⊥BF于点G,如图2,
∵点B关于直线l的对称点为C,∠BAC=2α,
∴BH=CH,∠BAH=∠CAH=α,
∵AH⊥BC,BD⊥AC,∴∠CAH+∠ACH=90°,∠CBD+∠ACH=90°,
∴∠CBD=∠CAH=α,
∵∠AEB![]() ,∠AEB=∠CBD+∠F,
,∠AEB=∠CBD+∠F,
∴∠F=45°,则△EFG为等腰直角三角形,∴![]() ,
,
∵∠BAH=∠EBG=α,∠AHB=∠BGE=90°,AB=BE,
∴△ABH≌△BEG(AAS),
∴BH=EG,
∵BC=2BH,∴BC=2EG=![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】已知BD平分∠ABF,且交AE于点D.
(1)求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);
(2)设AP交BD于点O,交BF于点C,连接CD,当AC⊥BD时,求证:四边形ABCD是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣a)(x﹣b),其中a<b,m、n(m<n)是方程1﹣(x﹣a)(x﹣b)=0的两个根,则实数a、b、m、n的大小关系是( )
A. a<m<n<b B. m<a<b<n C. a<m<b<n D. m<a<n<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D,E分别是AB,AC上的点,BE与CD交于点F,给出下列三个条件:①∠DBF=∠ECF;②∠BDF=∠CEF; ③BD=CE.两两组合在一起,共有三种组合:(1)①②;(2)①③;(3)②③问能判定AB=AC的组合的是( )
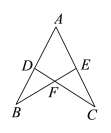
A.(1)(2)B.(1)(3)C.(2)(3)D.(1)(2)(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“求作∠AOB的角平分线”的尺规作图过程.

已知:如图,钝角∠AOB.求作:∠AOB的角平分线.
作法:
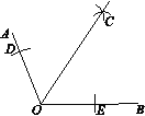
①在OA和OB上,分别截取OD、OE,使OD=OE;
②分别以D、E为圆心,大于![]() 的长为半径作弧,在∠AOB内,两弧交于点C;
的长为半径作弧,在∠AOB内,两弧交于点C;
③作射线OC.
所以射线OC就是所求作的∠AOB的角平分线.
在该作图中蕴含着几何的证明过程:
由①可得:OD=OE
由②可得:_________________
由③可知:OC=OC
∴______≌_________(依据:________________________)
∴可得∠COD=∠COE(全等三角形对应角相等)
即OC就是所求作的∠AOB的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】信息1:我们已经学完了解分式方程,它的一般步骤为:确定最简公分母、化为整式方程、求出整式方程的解、进行检验(第一,代入最简公分母验证是否为零,第二代入分式方程的左右两边检验是否相等)、确定分式方程的解.其中代入最简公分母验证这一步也就是在验证所有分式在取此值时是否有意义;
信息2:遇到![]() 这种特征的题目,可以两边同时平方得到
这种特征的题目,可以两边同时平方得到![]() ;
;
信息3:遇到![]() 这种特征的题目,可以将左边变形,得到
这种特征的题目,可以将左边变形,得到![]() ,进而可以得到
,进而可以得到![]() 或
或![]() .
.
结合上述信息解决下面的问题:
问题1:如果![]() .可得:
.可得:![]() ;
;
问题2:解关于b的方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①4a+b=0②9a+c>3b;③8a+7b+2c>0④若点A(﹣3,y1),点B(﹣2,y2),点C(8,y3)在该函数图象上,则y1<y3<y2⑤若方程a(x﹣1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣l<5<x2,其中正确的结论有( )
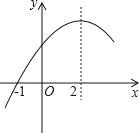
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
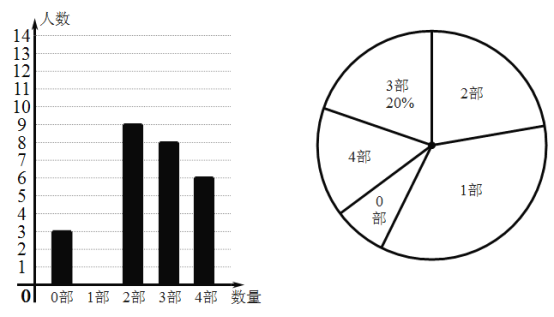
(1)本次抽样调查共抽取了_____名学生,并将条形统计图补充完整;
(2)本次调查所得数据的众数是_____部,中位数是_____部;
(3)计算该校抽取的这部分学生平均每人看“四大古典名著”多少部?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com