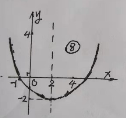
【题目】如图抛物线
（
），下列结论错误的是（ ）
A.a、b同号B.
C.
和
时，y值相同D.当
时，
【答案】A
【解析】
利用抛物线开口方向得到a＞0，利用抛物线的对称轴得到b=-4a＜0，则可对AB进行判断；利用抛物线的对称性可对C进行判断；利用抛物线的对称性确定抛物线与x轴的一个交点坐标为（5，0），再根据二次函数的图象可对D进行判断．
解：∵抛物线开口向上，
∴a＞0，
∵抛物线的对称轴为直线x=-
=2，
∴b=-4a＜0，所以A错误，
∴b+4a=0，所以B正确；
∵抛物线的对称轴为直线x=2，
∴当x=1和x=3时，函数值相等，所以C正确；
∵抛物线与x轴的一个交点坐标为（-1，0），
而抛物线的对称轴为直线x=2，
∴抛物线与x轴的一个交点坐标为（5，0），
∴当-1＜x＜5时，y＜0，所以D正确．
故选A.
科目：初中数学 来源： 题型：
【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．
下面有三个推断：
①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；
②随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；
③若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率一定是0.620．
其中合理的是（ ）
A. ① B. ② C. ①② D. ①③
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场购进一批单价为16元的日用品.若按每件23元的价格销售，每月能卖出270件；若按每件28元的价格销售，每月能卖出120件；若规定售价不得低于23元，假定每月销售件数y(件)与价格x（元/件）之间满足一次函数.
（1）试求y与x之间的函数关系式．
（2）在商品不积压且不考虑其他因素的条件下，销售价格定为多少时，才能使每月的毛利润w最大？每月的最大毛利润为多少？
（3）若要使某月的毛利润为1800元，售价应定为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
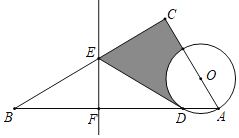
【题目】如图，在△ABC中，∠C＝90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若∠B＝30°，AC＝6，OA＝2，直接写出阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
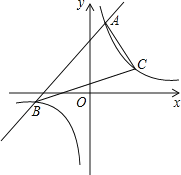
【题目】已知一次函数
的图象与反比例函数
的图象交于
两点，点
的坐标为
（1）求一次函数的解析式
（2）已知双曲线在第一象限上有一点到
到
轴的距离为3，求
的面积
查看答案和解析>>
科目：初中数学 来源： 题型：
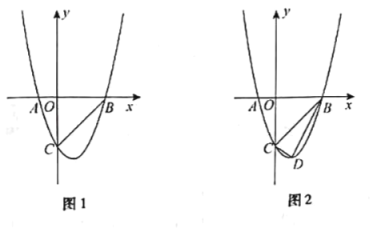
【题目】如图，在平面直角坐标系中，抛物线
交
轴于
，
两点，与
轴交于点
.连接
.
（1）求抛物线的解析式和点的坐标；
（2）“若点
为第四象限内抛物线上一动点，点的横坐标为
，
的面积为
，求关于的函数关系式，并求出的最大值；
（3）抛物线的对称轴上是否存在点
，使
为等腰三角形？若存在，请直接写出所有点的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
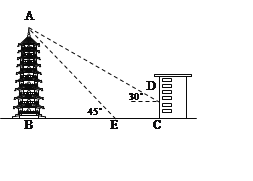
【题目】某风景区内有一古塔AB，在塔的北面有一建筑物，当光线与水平面的夹角是30°时，塔在建筑物的墙上留下了高3米的影子CD；而当光线与地面的夹角是45°时，塔尖A在地面上的影子E与墙角C有15米的距离（B、E、C在一条直线上），求塔AB的高度（结果保留根号）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
