练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将Rt△ABC（其中∠B=35°，∠C=90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C，A，B1在同一条直线上，那么旋转角等于（ ）
    A.55°
    B.70°
    C.125°
    D.145°

    【答案】C
    【解析】解：∵∠B=35°，∠C=90°， ∴∠BAC=90°﹣∠B=90°﹣35°=55°，
    ∵点C、A、B1在同一条直线上，
    ∴∠BAB′=180°﹣∠BAC=180°﹣55°=125°，
    ∴旋转角等于125°．
    故选C．
    【考点精析】解答此题的关键在于理解旋转的性质的相关知识，掌握①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若△ABC 的三个内角之比为 1:5:3，那么△ABC 中最大角的度数为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。

    (1)你认为图b中的阴影部分的正方形的边长等于多少?

    (2)请用两种不同的方法求图中阴影部分的面积。

    方法1：

    方法2：

    (3)观察图b你能写出下列三个代数式之间的等量关系吗?

    代数式:

    (4)根据（3）题中的等量关系，解决如下问题：

    若，则= 。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC交⊙O于点F．
    （1）AB与AC的大小有什么关系？为什么？
    （2）若∠BAC=70°，求弧BD、弧DF和弧AF的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知甲. 乙两车分别从相距300km的A. B两地同时出发，相向而行，其中甲到B地后立即返回，下图是它们离各自出发地的距离y（km）与行驶时间x（h）之间的函数图象.

    （1）求甲车离出发地的距离y与行驶时间x之间的函数关系式，并写出自变量的取值范围；

    （2）当它们行驶到与各自出发地的距离相等时甲用了4.5小时，求乙车离出发地的距离y与行驶时间x之间的函数关系式，并写出x的范围；

    （3）在（2）的条件下，求它们的行驶过程中相遇的时间.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果把存入3万元记作+3万元，那么支出2万元应记作__________， -4万元表示的意思是________________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a．小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（ ）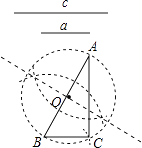
    A.勾股定理
    B.直径所对的圆周角是直角
    C.勾股定理的逆定理
    D.90°的圆周角所对的弦是直径

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，点， 分别是射线， 上两定点，且， ；动点从点向点运动，以为斜边向右侧作等腰直角．设线段的长，点到射线的距离为．

    （1）若，直接写出点到射线的距离；

    （2）求关于的函数表达式，并在图中画出函数图象；

    （3）当动点从点运动到点，求点运动经过的路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人同在如图所示的地下车库等电梯，两人到1至4层的任意一层出电梯，
    （1）请你用画树状图或列表法求出甲、乙二人在同一层楼出电梯的概率；
    （2）小亮和小芳打赌说：“若甲、乙在同一层或相邻楼层出电梯，则小亮胜，否则小芳胜”．该游戏是否公平？说明理由．

    查看答案和解析>>

    同步练习册答案