
【题目】已知,如图AB是圆O的直径,射线AM⊥AB于点A.点D在AM上,连接OD交圆O于点E,过点D作DC=DA.交圆O于点C(A,C不重合),连接BC,CE.
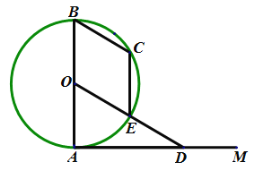
(1)求证:CD是圆O的切线;
(2)若四边形OECB是菱形,圆O的直径AB=2,求AD的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)依据SSS证明△OAD≌△OCD,从而得到∠OCD=∠OAD=90°;
(2)依据菱形的性质得到OE=CE,则△EOC为等边三角形,则∠CEO=60°,依据平行线的性质可知∠DOA=60°,利用特殊锐角三角函数可求得AD的长.
解:如图,连接OC,∵AM⊥AB,
∴∠OAD=90°.
∵OA=OC,OD=OD,AD=DC,
∴△OAD≌△OCD,
∴∠OCD=∠OAD=90°.
∴OC⊥CD,
∴CD是⊙O的切线.
(2)∵四边形OECB是菱形,
∴OE=CE.
又∵OC=OE,
∴OC=OE=CE.
∴∠CEO=60°.
∵CE∥AB,
∴∠AOD=60°.
在Rt△OAD中,∠AOD=60°,AO=![]() 1,
1,
∴AD=![]() .
.
故答案为:![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列四个判断:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果AD⊥BC且AB=AC,那么四边形AEDF是菱形.正确的个数是( )

A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).
对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求该抛物线的函数表达式及对称轴;
(2)设点![]() 关于原点的对称点为
关于原点的对称点为![]() ,点
,点![]() 是抛物线对称轴上一动点,记抛物线在
是抛物线对称轴上一动点,记抛物线在![]() ,
,![]() 之间的部分为图象
之间的部分为图象![]() (包含
(包含![]() ,
,![]() 两点),如果直线
两点),如果直线![]() 与图象
与图象![]() 有一个公共点,结合函数的图象,直接写出点
有一个公共点,结合函数的图象,直接写出点![]() 纵坐标
纵坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某二次函数的图象是一条顶点为P(4.-4)的抛物线,它经过原点和点A,它的对称轴交线段
OA于点M.点N在对移轴上,且点M、N关于点P对称,连接AN,ON
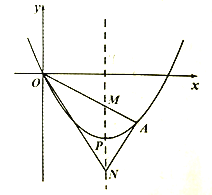
(1)求此二次函数的解析式:
(2)若点A的坐标是(6,-3).,请直接写出MN的长
(3)若点A在抛物线的对称轴右侧运动时,则∠ANM与∠ONM有什么数量关系?并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() .
.
(1)用含![]() 的式子表示
的式子表示![]() ;
;
(2)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的式子表示);
的式子表示);
(3)在(2)的条件下,已知点![]() ,若抛物线与线段
,若抛物线与线段![]() 恰有两个公共点,求
恰有两个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点
的顶点![]() 在定直线
在定直线![]() 上.
上.
(1)求![]() 点的坐标(用含
点的坐标(用含![]() 的式子表示);
的式子表示);
(2)求证:不论![]() 为何值,抛物线与定直线
为何值,抛物线与定直线![]() 的两交点间的距离
的两交点间的距离![]() 恒为定值;
恒为定值;
(3)当![]() 的顶点
的顶点![]() 在
在![]() 轴上,且与
轴上,且与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧)时,在
点左侧)时,在![]() 上是否存在两点
上是否存在两点![]() 、
、![]() ,设
,设![]() 交线段
交线段![]() 于
于![]() 点,使
点,使![]() ,且直线
,且直线![]() 将
将![]() 的面积分成
的面积分成![]() 的两部分?若存在,求出直线
的两部分?若存在,求出直线![]() 的解析式;若不存在,请说明理由.
的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
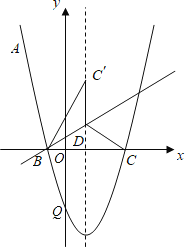
【题目】如图,抛物线y=ax2+bx﹣![]() 经过点A(﹣2,
经过点A(﹣2,![]() ),与x轴相交于B,C两点,且B点坐标为(﹣1,0).
),与x轴相交于B,C两点,且B点坐标为(﹣1,0).
(1)求抛物线的函数表达式;
(2)点D在抛物线的对称轴上,且位于x轴的上方,将△BCD沿直线BD翻折得到△BC′D,若点C′恰好落在抛物线的对称轴上,求点C′和点D的坐标;
(3)抛物线与y轴交于点Q,连接BQ,DQ,在抛物线上有一个动点P,且S△PBD=S△BDQ,求满足条件的点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com