
 已知四个数:a=(-2)2,b=-(-2),c=(-1)2013,d=-|-3|.
已知四个数:a=(-2)2,b=-(-2),c=(-1)2013,d=-|-3|.分析 (1)首先根据有理数的乘方的运算方法,求出a、c的值各是多少;然后根据一个数的相反数的求法,求出b的值是多少;最后根据一个数的绝对值的求法,求出d的值是多少即可.
(2)根据(1)求出的a、b、c、d的大小,把这四个数在数轴上分别表示出来即可.
(3)根据有理数大小比较的方法,用“<”把a、b、c、d,连接起来即可.
(4)首先分别求出|a|,|b|,|c|,|d|的值各是多少;然后根据有理数大小比较的方法,用“>”把|a|,|b|,|c|,|d|连接起来即可.
解答 解:(1)∵a=(-2)2,b=-(-2),c=(-1)2013,d=-|-3|,
a=4,b=2,c=-1,d=-3.
(2)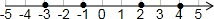 .
.
(3)∵-3<-1<2<4,
∴d<c<b<a.
(4)|a|=|4|=4,|b|=|2|=2,|c|=|-1|=1,|d|=|-3|=3,
∵1<2<3<4,
∴|c|<|b|<|d|<|a|.
故答案为:4、2、-1、-3;d<c<b<a;|c|<|b|<|d|<|a|.
点评 (1)此题主要考查了有理数大小比较的方法,要熟练掌握,解答此题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.
(2)此题还考查了数轴的特征和应用,要熟练掌握,解答此题的关键是要明确:一般来说,当数轴方向朝右时,右边的数总比左边的数大.


科目:初中数学 来源: 题型:解答题
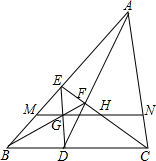 如图所示,已知D,E分别是△ABC的边BC,AB上的点,AD,CE交F,BF,DE交于G,过G作BC的平行线MN,交AB,CE,AC于M,H,N,求证:GH=NH.
如图所示,已知D,E分别是△ABC的边BC,AB上的点,AD,CE交F,BF,DE交于G,过G作BC的平行线MN,交AB,CE,AC于M,H,N,求证:GH=NH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
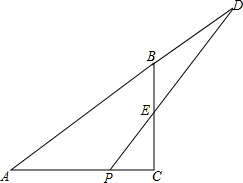 如图.在Rt△ABC中.∠ACB=90°,AB=10,BC:AC=3:4,点D在AB延长线上,BD=6,点P是AC上的-个动点.PD交BC于点E.设PC=x,S△PCE=y.
如图.在Rt△ABC中.∠ACB=90°,AB=10,BC:AC=3:4,点D在AB延长线上,BD=6,点P是AC上的-个动点.PD交BC于点E.设PC=x,S△PCE=y.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
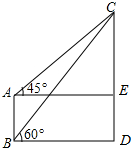 如图:从B处测得建筑物上旗杆EC顶点C的仰角是60°,再从B的正上方40米高层上A处,测得C的仰角是45°,那么旗杆顶点C离地CD的高度是( )米.
如图:从B处测得建筑物上旗杆EC顶点C的仰角是60°,再从B的正上方40米高层上A处,测得C的仰角是45°,那么旗杆顶点C离地CD的高度是( )米.| A. | 18$\sqrt{3}$+40 | B. | 19$\sqrt{3}$+50 | C. | 20$\sqrt{3}$+60 | D. | 21$\sqrt{3}$+70 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:已知AB是⊙O的直径,直线l与⊙O相切于点C,且弦CD⊥AB,垂足为E,BF⊥l,垂足为F,BF交⊙O于G.
如图:已知AB是⊙O的直径,直线l与⊙O相切于点C,且弦CD⊥AB,垂足为E,BF⊥l,垂足为F,BF交⊙O于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com