
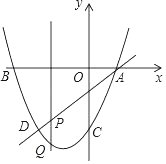
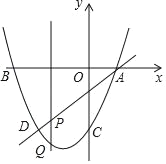
【题目】如图,抛物线y=x2+bx﹣3过点A(1,0),直线AD交抛物线于点D,点D的横坐标为﹣2,点P是线段AD上的动点.
(1)b= ,抛物线的顶点坐标为 ;
(2)求直线AD的解析式;
(3)过点P的直线垂直于x轴,交抛物线于点Q,连接AQ,DQ,当△ADQ的面积等于△ABD的面积的一半时,求点Q的坐标.
【答案】(1)2 (﹣1,﹣4);(2)y=x﹣1;(3)Q(0,﹣3)或(﹣1,﹣4).
【解析】
(1)将点A的坐标代入函数解析式求得b的值,然后利用配方法将函数解析式转化为顶点式,可以直接求得顶点坐标;
(2)结合(1)中抛物线解析式求得点D的坐标,利用点A、D的坐标来求直线AD解析式;
(3)由二次函数图象上点的坐标特征求得点B的坐标,易得AB=4.结合三角形面积公式求得S△ABD=6.设P(m,m﹣1),Q(m,m2+2m﹣3).则PQ=﹣m2﹣m+2.利用分割法得到:S△ADQ=S△APQ+S△DPQ=![]() PQ=
PQ=![]() (﹣m2﹣m+2).根据已知条件列出方程
(﹣m2﹣m+2).根据已知条件列出方程![]() (﹣m2﹣m+2)=3.通过解方程求得m的值,即可求得点Q的坐标.
(﹣m2﹣m+2)=3.通过解方程求得m的值,即可求得点Q的坐标.
解:(1)把A(1,0)代入y=x2+bx﹣3,得12+b﹣3=0.
解得b=2.
故该抛物线解析式为:y=x2+2x﹣3=(x+1)2﹣4,即y=(x+1)2﹣4.
故顶点坐标是(﹣1,﹣4).
故答案是:2;(﹣1,﹣4).
(2)由(1)知,抛物线解析式为:y=x2+2x﹣3.
当x=﹣2,则y=(﹣2)2+2×(﹣2)﹣3=﹣3,
∴点D的坐标是(﹣2,﹣3).
设直线AD的解析式为:y=kx+t(k≠0).
把A(1,0),D(﹣2,﹣3)分别代入,得![]() .
.
解得![]() .
.
∴直线AD的解析式为:y=x﹣1;
(3)当y=0时,x2+2x﹣3=0,
解得x1=1,x2=﹣3,
∴B(﹣3,0),
∴AB=4.
∴S△ABD=![]() ×4×3=6.
×4×3=6.
设P(m,m﹣1),Q(m,m2+2m﹣3).
则PQ=(m﹣1)﹣(m2+2m﹣3)=﹣m2﹣m+2.
∴S△ADQ=S△APQ+S△DPQ=![]() PQ(1﹣m)+
PQ(1﹣m)+![]() PQ(m+2)=
PQ(m+2)=![]() PQ=
PQ=![]() (﹣m2﹣m+2).
(﹣m2﹣m+2).
当△ADQ的面积等于△ABD的面积的一半时,![]() (﹣m2﹣m+2)=3.
(﹣m2﹣m+2)=3.
解得m1=0,m2=﹣1.
∴Q(0,﹣3)或(﹣1,﹣4).


科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(2k﹣1)x+k2+1=0有两个不相等的实数根x1,x2.
(1)求实数k的取值范围;
(2)若方程的两实数根x1,x2满足|x1|+|x2|=x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,按如下步骤作图:第一步,分别以点A、D为圆心,以大于![]() 的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )
的长为半径在AD的两侧作弧,交于两点M、N;第二步,连结MN,分别交AB、AC于点E、F;第三步,连结DE、DF..若BD=6,AF=4,CD=3,则BE的长是( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
(1)求证:△ABC≌△ABF;
(2)填空:
①当∠CAB= °时,四边形ADFE为菱形;
②在①的条件下,BC= cm时,四边形ADFE的面积是6![]() cm2.
cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
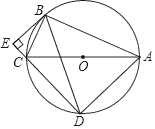
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,BD=BA,BE⊥DC交DC的延长线于点E.
(1)若∠BAD=70°,则∠BCA= °;
(2)若AB=12,BC=5,求DE的长:
(3)求证:BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
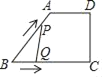
【题目】如图,在四边形ABCD中,AD∥BC,DC⊥BC,DC=4cm,BC=6cm,AD=3cm,动点P,Q同时从点B出发,点P以2cm/s的速度沿折线BA﹣AD﹣DC运动到点C,点Q以1cm/s的速度沿BC运动到点C,设P,Q同时出发xs时,△BPQ的面积为ycm2.则y与x的函数图象大致是( )
A. 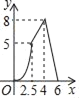 B.
B. 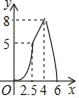 C.
C. 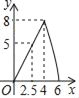 D.
D. 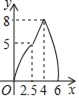
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 是
是![]() 的延长线上一点,且∠PDB=
的延长线上一点,且∠PDB=![]() ∠A,连接
∠A,连接![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)填空:
①当![]() 的度数为______时,四边形
的度数为______时,四边形![]() 是菱形;
是菱形;
②当![]() 时,
时,![]() 的面积为_________.
的面积为_________.
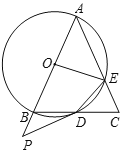
查看答案和解析>>
科目:初中数学 来源: 题型:
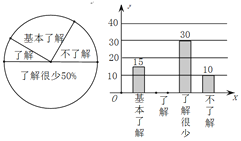
【题目】济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有_____人,扇形统计围中“基本了解”部分所对应扇形的圆心角为______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数;
(4)从对食品安全知识达到“了解”的3个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com