
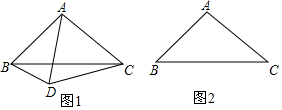
分析 (1)由∠BAC=100°,AB=AC,可以确定∠ABC=∠ACB=40°,旋转角为α,α=60°时△ACD是等边三角形,且AC=AD=AB=CD,知道∠BAD的度数,进而求得∠CBD的大小;
(2)根据旋转的定义即可得.
(3)结合(1)(2)的解题过程可以发现规律,△ACD是等边三角形时,CD在△ABC内部时,CD在△ABC外部时,求得答案
解答 解:(1)∵∠BAC=100°,AB=AC,
∴∠ABC=∠ACB=40°,当α=60°时,
由旋转的性质得AC=CD,
∴△ACD是等边三角形,
∴∠DAC=60°,
∴∠BAD=∠BAC-∠DAC=100°-60°=40°,
∵AB=AC,AD=AC,
∴∠ABD=∠ADB=$\frac{180°-∠BAD}{2}$=70°,
∴∠CBD=∠ABD-∠ABC=70°-40°=30°,
故答案为:30°;
(2)如图2所示;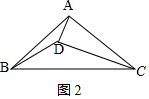
(3)①由(1)可知,∠α=60°时可得∠BAD=100°-60°=40°,∠ABC=∠ACB=90°-$\frac{100°}{2}$=40°,
∠ABD=90°-$\frac{1}{2}$∠BAD=120°-$\frac{100°}{2}$=70°,
∠CBD=∠ABD-∠ABC=30°.
②如图3,翻折△BDC到△BD1C,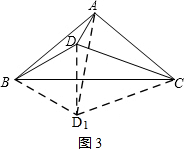
则此时∠CBD1=30°,
∠BCD=60°-∠ACB=$\frac{100°}{2}$-30°=20°,
∠α=∠ACB-∠BCD1=∠ACB-∠BCD=$\frac{180°-100°}{2}$-20°=20°;
③以C为圆心CD为半径画圆弧交BD的延长线于点D2,连接CD2,
∠CDD2=∠CBD+∠BCD=30°+$\frac{100°}{2}$-30°=50°,
∠DCD2=180°-2∠CDD2=180°-100°=80°,
∠α=60°+∠DCD2=140°.
综上所述,α为60°或20°或140°时,∠CBD=30°.
点评 本题考查旋转变换的定义及性质、等腰三角形的性质,解答这类题目的关键是要善于从探究特殊结论中归纳出一般性解题方法,并灵活运用这种方法解答一般性的问题,真正达到举一反三的目的.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
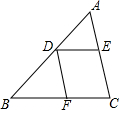 如图,在△ABC中,D是AB边上一点,DE∥BC,DF∥AC,下列结论正确的是( )
如图,在△ABC中,D是AB边上一点,DE∥BC,DF∥AC,下列结论正确的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{AC}$ | B. | $\frac{DE}{BF}$=$\frac{AE}{AC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{AD}{BD}$=$\frac{DF}{AC}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
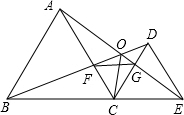 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正确的结论有( )个.
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AO=BF;③FG∥BE;④∠BOC=∠EOC;⑤BO=OC+AO,其中正确的结论有( )个.| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com