
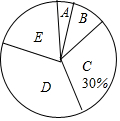
 为了了解某校九年级(1)班学生的体育测试情况,对全班学生的体育成绩进行了统计,并绘制出以下不完整的频数分布表和扇形统计图
为了了解某校九年级(1)班学生的体育测试情况,对全班学生的体育成绩进行了统计,并绘制出以下不完整的频数分布表和扇形统计图| 分组 | 分数段(分) | 频数 |
| A | 36≤x<41 | 2 |
| B | 41≤x<46 | 5 |
| C | 46≤x<51 | 15 |
| D | 51≤x<56 | m |
| E | 56≤x<61 | 10 |
分析 (1)利用C组学生频数除以C组学生所占百分比即可得到全班学生人数,利用学生总数减去A、B、C、E四段的频数即可得到m的值;
(2)根据中位数定义:将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数可确定中位数应是第25与26名学生成绩的平均数,进而可得答案;
(3)首先画出树状图可以得到答案.
解答 解:(1)全班学生人数:15÷30%=50(人),
m=50-2-5-15-10=18;
(2)中位数应是第25与26名学生成绩的平均数,
所以中位数为51≤x<56内;
(3)画树状图: ,
,
所以共有6种结果,其中一男一女的结果有4种,
所以P(一男一女)=$\frac{4}{6}$=$\frac{2}{3}$.
点评 此题主要考查了中位数、频数分布,扇形图表和概率的求法.关键是掌握概率=所求情况数与总情况数之比,能正确从统计图中得到信息.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com