
【题目】已知二次函数y=﹣2x2+bx+c的图象经过点(0,6)和(1,8).
(1)求这个二次函数的解析式;
(2)①当x在什么范围内时,y随x的增大而增大?
②当x在什么范围内时,y>0?
【答案】(1)y=﹣2x2+4x+6;(2)①当x<1时,y随x的增大而增大;②当﹣1<x<3时,y>0
【解析】
(1)根据二次函数y=﹣2x2+bx+c的图象经过点(0,6)和(1,8),可以求得该抛物线的解析式;
(2)①根据(1)求得函数解析式,将其化为顶点式,然后根据二次函数的性质即可得到x在什么范围内时,y随x的增大而增大;
②根据(1)中的函数解析式可以得到x在什么范围内时,y>0.
(1)∵二次函数y=﹣2x2+bx+c的图象经过点(0,6)和(1,8),
∴![]() ,得
,得![]() ,
,
即该二次函数的解析式为y=﹣2x2+4x+6;
(2)①∵y=﹣2x2+4x+6=﹣2(x﹣1)2+8,
∴该函数的对称轴是x=1,函数图象开口向下,
∴当x<1时,y随x的增大而增大;
②当y=0时,0=﹣2x2+4x+6=﹣2(x﹣3)(x+1),
解得,x1=3,x2=﹣1,
∴当﹣1<x<3时,y>0.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
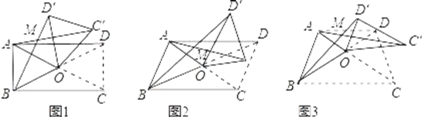
【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠DOC=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.
(1)当四边形ABCD是矩形时,如图1,请猜想AC′与BD′的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
(2)当四边形ABCD是平行四边形时,如图2,已知AC=kBD,请猜想此时AC′与BD′的数量关系以及∠AMB与α的大小关系,并证明你的猜想;
(3)当四边形ABCD是等腰梯形时,如图3,AD∥BC,此时(1)AC′与BD′的数量关系是否成立?∠AMB与α的大小关系是否成立?不必证明,直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
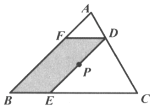
【题目】如图,已知点P是△ABC的重心,过P作AB的平行线DE,分别交AC于点D,交BC于点E,作DF//BC,交AB于点F,若四边形BEDF的面积为4,则△ABC的面积为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
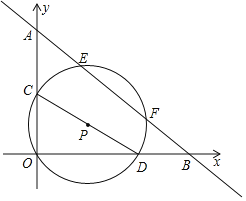
【题目】如图,点A,B的坐标分别为(0,8),(10,0),动点C,D分别在OA,OB上且CD=8,以CD为直径作⊙P交AB于点E,F.动点C从点O向终点A的运动过程中,线段EF长的变化情况为( )
A.一直不变B.一直变大
C.先变小再变大D.先变大再变小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=4,BC=8,∠ABC=60°.点P是边BC上一动点,作△PAB的外接圆⊙O交BD于E.
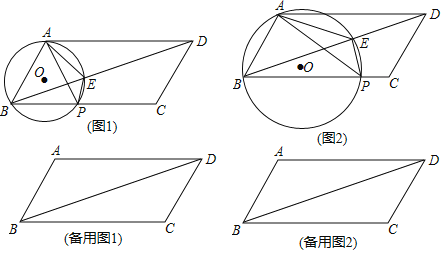
(1)如图1,当PB=3时,求PA的长以及⊙O的半径;
(2)如图2,当∠APB=2∠PBE时,求证:AE平分∠PAD;
(3)当AE与△ABD的某一条边垂直时,求所有满足条件的⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
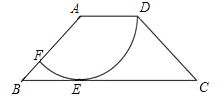
【题目】如图,在四边形ABCD中,AD∥BC,AD=2,AB=![]() ,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.
(1)求∠ABE的大小及![]() 的长度;
的长度;
(2)在BE的延长线上取一点G,使得![]() 上的一个动点P到点G的最短距离为
上的一个动点P到点G的最短距离为![]() ,求BG的长.
,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
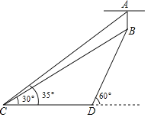
【题目】如图,宾馆大厅的天花板上挂有一盏吊灯AB,某人从C点测得吊灯顶端A的仰角为![]() ,吊灯底端B的仰角为
,吊灯底端B的仰角为![]() ,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为
,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为![]() .请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,
.请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AC和BC为腰向外作等腰直角△DAC和等腰直角△EBC,连接DE.

(1)求证:△DAC∽△EBC;
(2)求△ABC与△DEC的面积比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com