
【题目】如图,在ΔABC中,∠BAC=120°,点D是BC上一点,BD的垂直平分线交AB于点E,将ΔACD沿AD折叠,点C恰好与点E重合,则∠B等于( )
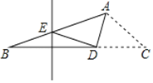
A.15°B.20°C.25°D.30°
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
京通公交快速通道开通后,为响应市政府“绿色出行”的号召,家住通州新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米.他用乘公交车的方式平均每小时行驶的路程比他自用驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的![]() .小王用自驾车方式上班平均每小时行驶多少千米?
.小王用自驾车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
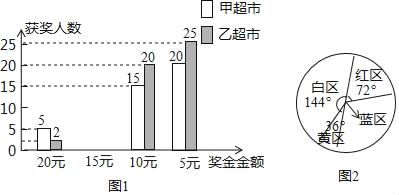
【题目】两家超市同时采取通过摇奖返现金搞促销活动,凡在超市购物满100元的顾客均可以参加摇奖一次.小明和小华对两家超市摇奖的50名顾客获奖情况进行了统计并制成了图表(如图)
奖金金额 获奖人数 | 20元 | 15元 | 10元 | 5元 |
商家甲超市 | 5 | 10 | 15 | 20 |
乙超市 | 2 | 3 | 20 | 25 |
(1)在甲超市摇奖的顾客获得奖金金额的中位数是 ,在乙超市摇奖的顾客获得奖金金额的众数是 ;
(2)请你补全统计图1;
(3)请你分别求出在甲、乙两超市参加摇奖的50名顾客平均获奖多少元?
(4)图2是甲超市的摇奖转盘,黄区20元、红区15元、蓝区10元、白区5元,如果你购物消费了100元后,参加一次摇奖,那么你获得奖金10元的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于2微克/毫升的持续时间多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
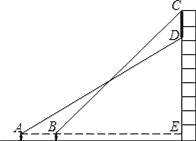
【题目】如图所示,小杨在广场上的A处正面观测一座楼房墙上的广告屏幕,测得屏幕下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该屏幕上端C处的仰角为45°.若该楼高为26.65m,小杨的眼睛离地面1.65m,广告屏幕的上端与楼房的顶端平齐.求广告屏幕上端与下端之间的距离.(![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:![]()
(2)计算:3a(2a2-9a+3)-4a(2a-1)
(3)计算:(![]() )×(
)×(![]() )+|
)+|![]() -1|+(5-2π)0
-1|+(5-2π)0
(4)先化简,再求值:(xy2+x2y)![]() ,其中x=
,其中x=![]() ,y=
,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
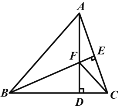
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
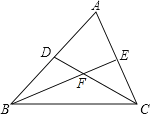
【题目】如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F.
(1)∠ABC=40°,∠A=60°,求∠BFD的度数;
(2)直接写出∠A与∠BFD的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com