
����Ŀ��ij�̵����� A��B ����Ʒ�ƵIJ�ɫ���ӻ���A��B ���ֲʵ�Ľ���ÿ̨�ֱ�Ϊ2000 Ԫ��1600Ԫ��һ �� �� A��B �� �� �� �� ÿ ̨ �� �� �� �� �� Ϊ 2700 Ԫ��2100 Ԫ���� �� �� Ϊ 12000Ԫ��Ϊ�����������·�Ӫ����Ա�ṩ���������۲��ԣ�
����һ�� A �ֲʵ�ÿ̨����100Ԫ��B �ֲʵ�ÿ̨����80Ԫ���������������ֱ�����30%��40%��
���Զ��� A �ֲʵ�ÿ̨���� 150 Ԫ��B �ֲʵ�ÿ̨���� 100 Ԫ��������������������50%��
����������Ϣ������и��⣺
��1����һ�·� A��B ���ֲʵ����������
��2�����·������ֲ����Ƿ�����������
��3�����·ݸ��̵�Ӧ�ò��������������۲����е���һ�֣�����ʹ�̵�����õ�����϶ࣿ��˵�����ɣ�
���𰸡���1��![]() ��
��![]() ��
��![]() ����2�����·������ֲ��Զ�����������3���̵�Ӧ���ò��Զ�ʹ�̵�������϶࣮
����2�����·������ֲ��Զ�����������3���̵�Ӧ���ò��Զ�ʹ�̵�������϶࣮
��������
��1����һ�·�A��B���ֲʵ��������ֱ�Ϊ![]() ̨��
̨��![]() ̨����ô
̨����ô![]() �ʵ��������Ϊ��
�ʵ��������Ϊ��![]() ��
��![]() �ʵ��������Ϊ:
�ʵ��������Ϊ:![]() �������������г���Ԫһ�η��̣�����Ȼ���⼴�ɣ�
�������������г���Ԫһ�η��̣�����Ȼ���⼴�ɣ�
��2�����ղ���һ�ķ�������ʱ![]() �ʵ���ۼ�Ϊ
�ʵ���ۼ�Ϊ![]() ����������Ϊ
����������Ϊ![]() ��
��![]() �ʵ���ۼ�Ϊ
�ʵ���ۼ�Ϊ![]() , ��������Ϊ
, ��������Ϊ![]() �����ɱ�ʾ����ʱ���������ղ��Զ��ķ�������ʱ
�����ɱ�ʾ����ʱ���������ղ��Զ��ķ�������ʱ![]() �ʵ���ۼ�Ϊ
�ʵ���ۼ�Ϊ![]() ����������Ϊ
����������Ϊ![]() ��
��![]() �ʵ���ۼ�Ϊ
�ʵ���ۼ�Ϊ![]() ����������Ϊ
����������Ϊ![]() �����ɱ�ʾ����ʱ�������ֱ��ô�ʱ�����������һ�µ�����Ƚϴ�С������⣻
�����ɱ�ʾ����ʱ�������ֱ��ô�ʱ�����������һ�µ�����Ƚϴ�С������⣻
��3�����ݣ�2���п��Եõ����ֲ��������������ӣ�����ֻ��Ҫ�Ƚ������ֲ����µ������С������⣻
�⣺��1����һ�·�A��B���ֲʵ��������ֱ�Ϊx̨��y̨����������ã�
![]()
![]()
![]()
��![]()
![]() ��Ϊ��Ȼ��
��Ϊ��Ȼ��
![]()
![]() ��
��![]() ��
��![]()
��1�������һ������Ϊ![]() �����Զ�������Ϊ
�����Զ�������Ϊ![]()
![]()
![]()
![]() ��
�� ![]()
![]() ���·������ֲ��Զ�����������
���·������ֲ��Զ�����������
��3��![]()
![]()
![]()
![]()
![]() �̵�Ӧ���ò��Զ�ʹ�̵�������϶࣮
�̵�Ӧ���ò��Զ�ʹ�̵�������϶࣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
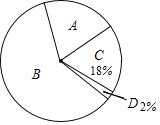
����Ŀ��ij��ѧ��һ����ѧ��ȤС���ڱ�Уѧ���п�չ������Ϊ������֪��������ר�������������ȡ��������ķ�ʽ�����ʾ����飬�ʾ�����Ľ����Ϊ��A���dz��˽�������B���Ƚ��˽�������C�������˽�������D����̫�˽����ĸ��ȼ������������ݽ����������Ƴ�����������������ͳ��ͼ����������ͼ���е���Ϣ�����������
�ȼ� | A | B | C | D |
Ƶ�� | 40 | 120 | 36 | n |
Ƶ�� | 0.2 | m | 0.18 | 0.02 |
��1������m���� ����n���� ����
��2������ͳ��ͼ�У�A��������Ӧ�����ε�Բ�Ľ����� ����������ȡѧ���Զ������˽�̶ȵ��������� ����
��3������У����ѧ��1500�ˣ�����ݵ�����������Щѧ�������Ƚ��˽�������ԼΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������a��b��c����Ma��b��c��ʾ������������λ������maxa��b��c��ʾ��������������������磺M2��1��01��max2��1��00��max2��1��a![]() ������⣺Msin45��cos60��tan60_____�����max3��53x��2x63����x��ȡֵ��ΧΪ______��
������⣺Msin45��cos60��tan60_____�����max3��53x��2x63����x��ȡֵ��ΧΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ϵ�У�O��0��0����A��3��3![]() ����B��6��0��������OAB��ֱ��CD�۵���ʹ��Aǡ�������߶�OB�ϵĵ�E������OE��
����B��6��0��������OAB��ֱ��CD�۵���ʹ��Aǡ�������߶�OB�ϵĵ�E������OE��![]() ����AC��AD��ֵ�ǣ� ��
����AC��AD��ֵ�ǣ� ��
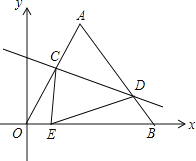
A.1��2B.2��3C.6��7D.7��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
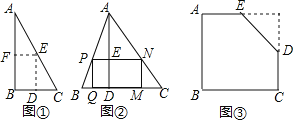
����Ŀ����ͼ�٣���һ��ֱ��������ֽƬ����B��90����AB��12��BC��8��С������м���һ���ԡ�BΪ�ڽ���������ľ��Σ������������֣���������λ��DE��EF����ʱ�����õľ��ε�������
��1����ͨ������˵��С���IJ����Ƿ���ȷ��
��2����ͼ�ڣ��ڡ�ABC�У�BC��10��BC���ϵĸ�AD��10������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ������PQMN��������ֵ��
��3����ͼ�ۣ��������ABCDE�У�AB��16��BC��20��AE��10��CD��8����A����B����C��90����С�����м�����һ��������ľ��Σ���BΪ���������ε��ڽǣ�����þ��ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
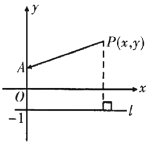
����Ŀ�����������˹(Apollonius of Perga��Լ��Ԫǰ262-190��)����ϣ����ѧ�ң���ŷ����ã�����������������������Բ�����ۡ��ǹŴ������ԵĿ�ѧ�ɹ�.
���ϣ���Բ�����ۡ�����������ߵĶ��壺ƽ����һ�����㵽һ��������һ����ֱ�ߵľ���֮�ȵ���1������˵��ƽ����һ���㵽һ������һ��ֱ�ߵľ�����ȵĹ켣����������.
���⣺��֪��![]() ��
��![]() ��ֱ��
��ֱ��![]() ������
������![]() ������
������![]() ��ֱ��
��ֱ��![]() �ľ�����
�ľ�����![]() �ij���ȣ������
�ij���ȣ������![]() ��
��![]() �Ĺ�ϵʽ.
�Ĺ�ϵʽ.
�⣺��ͼ����![]() ��
��![]() ��
��
��![]()
��![]() ��ֱ��
��ֱ��![]() ��
��
���![]() ��ֱ��
��ֱ��![]() �ľ���Ϊ
�ľ���Ϊ![]()
�ߵ�![]() ��ֱ��
��ֱ��![]() �ľ�����
�ľ�����![]() �ij���ȣ�
�ij���ȣ�
��![]() ��
��
ƽ������ã�![]() .
.
��������������![]() �������Ϊ
�������Ϊ![]() ��ֱ��
��ֱ��![]() ��Ϊ
��Ϊ![]() �������������˼·�������
�������������˼·�������![]() ��
��![]() �Ĺ�ϵʽ������ƽ��ֱ������ϵ��������㷨������ͼ�����ܷ���ʲô��
�Ĺ�ϵʽ������ƽ��ֱ������ϵ��������㷨������ͼ�����ܷ���ʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx��16��ͼ���㣨��2����40���͵㣨6��8����
��1����������κ���ͼ����x��Ľ������ꣻ
��2����y��0ʱ��ֱ��д���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
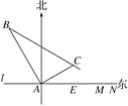
����Ŀ����ij�ɻ�����������ĵ���l����һ��Ϊ1 km�ķɻ��ܵ�MN(��ͼ)�����ܵ�MN��������14.5ǧ�״���һ�۲�վA.ijʱ�̲��һ������ֱ�߽���ķɻ�λ�ڵ�A�ı�ƫ��30���������A���15ǧ��B��������1���ӣ��ֲ�ø÷ɻ�λ�ڵ�A�ı�ƫ��60���������A���5![]() ǧ��C����
ǧ��C����
(1)�÷ɻ����е��ٶ��Ƕ���ǧ��/Сʱ��(�����������)
(2)����÷ɻ����ı亽��������У���ô�ɻ��ܷ������ܵ�MN֮�䣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2+bx+c��a��0���IJ���ͼ����ͼ��ʾ��ͼ����㣨��1��0�����Գ���Ϊֱ��x��1�����н��ۣ���2a+b��0����9a+c��3b��������A����3��y1������B����![]() ��y2������C��
��y2������C��![]() ��y3���ڸú���ͼ���ϣ���y1��y3��y2����������ax2+bx+c����3��a��0��������Ϊx1��x2����x1��x2����x1����1��3��x2����m��am+b����b��a��������ȷ�Ľ����У�������
��y3���ڸú���ͼ���ϣ���y1��y3��y2����������ax2+bx+c����3��a��0��������Ϊx1��x2����x1��x2����x1����1��3��x2����m��am+b����b��a��������ȷ�Ľ����У�������
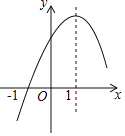
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com