
【题目】如图形似“w”的函数是由抛物线y1的一部分,其表达式为:y1=![]() (x2﹣2x﹣3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
(x2﹣2x﹣3)(x≤3)以及抛物线y2的一部分所构成的,其中曲线y2与曲线y1关于直线x=3对称,A、B是曲线y1与x轴两交点(A在B的左边),C是曲线y1与y轴交点.
(1)求A,B,C三点的坐标和曲线y2的表达式;
(2)我们把其中一条对角线被另一条对角线垂直且平分的四边形称为筝形.过点C作x轴的平行线与曲线y1交于另一个点D,连接AD.试问:在曲线y2上是否存在一点M,使得四边形ACDM为筝形?若存在,计算出点M的横坐标,若不存在,说明理由.

【答案】(1)A(﹣1,0),B(3,0),C(0,﹣![]() ).y2=
).y2=![]() (x2﹣10x+21)(x≥3);(2)存在,xM=
(x2﹣10x+21)(x≥3);(2)存在,xM=![]() .
.
【解析】
试题分析:(1)根据y1的解析式求出A,B,C三点坐标,再根据曲线y2与曲线y1关于直线x=3对称,求出y2与x轴的交点坐标,最后由待定系数法求出函数y2解析式即可;(2)先确定出点P的坐标和CP的解析式,然后与y2解析式形成方程,从而求出M点的横坐标.
试题解析:(1)根据y1的解析式求出A,B,C三点坐标,在y1=![]() (x2﹣2x﹣3)中,令y1=0,则有
(x2﹣2x﹣3)中,令y1=0,则有![]() (x2﹣2x﹣3)=0,解得x=﹣1或x=3,∴A(﹣1,0),B(3,0),∵C为曲线y1与y轴的交点,∴C(0,﹣
(x2﹣2x﹣3)=0,解得x=﹣1或x=3,∴A(﹣1,0),B(3,0),∵C为曲线y1与y轴的交点,∴C(0,﹣![]() ).又∵曲线y1与曲线y2关于直线x=3对称,∴曲线y2与x轴两交点坐标分别为(3,0)与(7,0),因为两抛物线形状相同,所以a值相同,∴y2=
).又∵曲线y1与曲线y2关于直线x=3对称,∴曲线y2与x轴两交点坐标分别为(3,0)与(7,0),因为两抛物线形状相同,所以a值相同,∴y2=![]() (x﹣3)(x﹣7)=
(x﹣3)(x﹣7)=![]() (x2﹣10x+21)(x≥3);(2)如图,
(x2﹣10x+21)(x≥3);(2)如图,
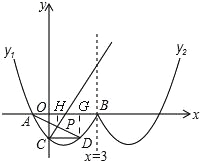
过点D作DG⊥x轴,过点P作PH⊥x轴,∴PH=![]() DG=
DG=![]() ,AH=
,AH=![]() AG=
AG=![]() ,∴OH=AH﹣AO=
,∴OH=AH﹣AO=![]() ,∴P(
,∴P(![]() ,
,![]() ),∴设线段AD的垂直平分线CP的解析式为y=kx+m,∵点C(0,﹣
),∴设线段AD的垂直平分线CP的解析式为y=kx+m,∵点C(0,﹣![]() ),∴
),∴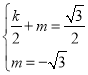 ,∴
,∴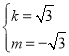 ,∴CP的解析式为y=
,∴CP的解析式为y=![]() x﹣
x﹣![]() ,若直线CP与曲线y2=
,若直线CP与曲线y2=![]() (x2﹣10x+21)(x≥3)有交点,则
(x2﹣10x+21)(x≥3)有交点,则![]() (x2﹣10x+21)=
(x2﹣10x+21)=![]() x﹣
x﹣![]() ,化简得:
,化简得:![]() ,解得:x=
,解得:x=![]() 或x=
或x=![]() (舍去,∵x<3).∴xM=
(舍去,∵x<3).∴xM=![]() .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A. 明天是晴天
B. 购买一张彩票,中奖
C. 经过有交通信号灯的路口,遇到红灯
D. 任意画出一个等边三角形,它是轴对称图形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【特例发现】如图1,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.求证:EP=FQ.
【延伸拓展】如图2,在△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB,AC为直角边,向△ABC外作Rt△ABE和Rt△ACF,射线GA交EF于点H.若AB=kAE,AC=kAF,请思考HE与HF之间的数量关系,并直接写出你的结论.
【深入探究】如图3,在△ABC中,G是BC边上任意一点,以A为顶点,向△ABC外作任意△ABE和△ACF,射线GA交EF于点H.若∠EAB=∠AGB,∠FAC=∠AGC,AB=kAE,AC=kAF,上一问的结论还成立吗?并证明你的结论.
【应用推广】在上一问的条件下,设大小恒定的角∠IHJ分别与△AEF的两边AE、AF分别交于点M、N,若△ABC为腰长等于4的等腰三角形,其中∠BAC=120°,且∠IHJ=∠AGB=θ=60°,k=2;
求证:当∠IHJ在旋转过程中,△EMH、△HMN和△FNH均相似,并直接写出线段MN的最小值(请在答题卡的备用图中补全作图).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多边形图案在一个有放大功能的复印机上复印出来,它的一条边由原来的1cm变成了2cm,那么它的面积会由原来的6cm2变为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com