
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬A (16£¬0)”¢C (0£¬8)£¬ĖıߊĪOABCŹĒ¾ŲŠĪ£¬D”¢E·Ö±šŹĒOA”¢BC±ßÉĻµÄµć£¬ŃŲ×ÅDEÕŪµž¾ŲŠĪ£¬µćAĒ”ŗĆĀäĶłyÖįÉĻµÄµćC“¦£¬µćBĀäŌŚµćB'“¦”£
(1) ĒóD”¢EĮ½µćµÄ×ų±ź£»
(2) ·“±ČĄżŗÆŹży =![]() (k >0) ŌŚµŚŅ»ĻóĻŽµÄĶ¼Ļń¾¹żEµć£¬ÅŠ¶ĻB”äŹĒ·ńŌŚÕāøö·“±ČĄżŗÆŹżµÄĶ¼ĻńÉĻ? ²¢ĖµĆ÷ĄķÓÉ£»
(k >0) ŌŚµŚŅ»ĻóĻŽµÄĶ¼Ļń¾¹żEµć£¬ÅŠ¶ĻB”äŹĒ·ńŌŚÕāøö·“±ČĄżŗÆŹżµÄĶ¼ĻńÉĻ? ²¢ĖµĆ÷ĄķÓÉ£»
(3) µćFŹĒ (2) ÖŠ·“±ČĄżŗÆŹżµÄĶ¼ĻńÓėŌ¾ŲŠĪµÄAB±ßµÄ½»µć£¬µćGŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŌµćD”¢E”¢F”¢GĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ,ĒóGµćµÄ×ų±ź£®(Ö±½ÓŠ“³ö“š°ø)

”¾“š°ø”æ£Ø1£©E£Ø10£¬8£©£Ø2£©²»ŌŚ£»£Ø3£©G1£Ø20£¬13£©”¢G2£Ø12£¬-3£©”¢G3£Ø0£¬3£©
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©ÉčOD=m£¬ŌņCD=DA=16-m£¬ŌŚRt”÷CODÖŠ£¬Óɹ“¹É¶ØĄķæɵĆm=6£¬¼“æɵĆDµÄ×ų±ź£¬ŌŁøł¾Ż¾ŲŠĪµÄŠŌÖŹ£¬æɵĆCE=CD=10£¬æɵĆEµÄ×ų±ź£»
£Ø2£©¹żB”ä×÷B”äM”ĶBCÓŚM£¬Ņ×µĆB”äMÓėCMµÄ³¤£¬½ų¶ųæɵĆkµÄÖµ£¬øł¾ŻĢāŅā£¬æɵƓš°ø£»
£Ø3£©øł¾ŻĢāŅā£¬·ÖČżÖÖĒéæöĢÖĀŪ£¬æɵĆŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ“ęŌŚG1”¢G2”¢G3µÄ×ų±ź£¬½ų¶ųæɵƓš°ø£®
ŹŌĢā½āĪö£ŗ£Ø1£©OA=16£¬OC=8£¬
ÉčOD=m£¬ŌņCD=DA=16-m
ŌŚRt”÷CODÖŠ£¬”ĻCOD=90”ć
ӧCD2=OC2+OD2
”ą£Ø16-m£©2=82+m2
½āµĆm=6£¬
”ąD£Ø6£¬0£©
”ßĖıߊĪOABCŹĒ¾ŲŠĪ
”ąOA”ĪCB
”ą”ĻCED=”ĻEDA
”ß”ĻEDA=”ĻCDE
”ą”ĻCED=”ĻCDE
”ąCE=CD=10£¬E£Ø10£¬8£©
£Ø2£©ČēĶ¼£¬¹żB”ä×÷B”äM”ĶBCÓŚM
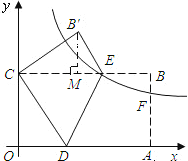
”ßB”äC=AB=8£¬B”äE=BE=6£¬”ĻCB”äE=90”ć
”ąB”äM=![]() £¬B”ä£Ø6.4£¬12.8£©
£¬B”ä£Ø6.4£¬12.8£©
”ßk=10”Į8=80£¬y£½![]()
ÓÖ”ß6.4”Į12.8”Ł80
”ąµćB”ä²»ŌŚÕāøö·“±ČĄżŗÆŹżµÄĶ¼ĻóÉĻ
£Ø3£©µ±x=16Ź±£¬y=5
”ąF£Ø16£¬5£©
ÓŠČżÖÖĒéæöČēĶ¼£ŗ
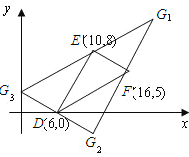
¢Ł°ŃĻ߶ĪDEĻČĻņÓŅĘ½ŅĘ10øöµ„Ī»³¤¶Č£¬ŌŁĻņÉĻĘ½ŅĘ5øöµ„Ī»£¬¶ĖµćEĀäŌŚG1“¦£¬G1£Ø20£¬13£©£»
¢Ś°ŃĻ߶ĪEFĻČĻņ×óĘ½ŅĘ4øöµ„Ī»³¤¶Č£¬ŌŁĻņĻĀĘ½ŅĘ8øöµ„Ī»£¬¶ĖµćFĀäŌŚG2“¦£¬G2£Ø12£¬-3£©£»
¢Ū°ŃĻ߶ĪDFĻČĻņ×óĘ½ŅĘ6øöµ„Ī»³¤¶Č£¬ŌŁĻņÉĻĘ½ŅĘ3øöµ„Ī»£¬¶ĖµćDĀäŌŚG3“¦£¬G3£Ø0£¬3£©£®
×ŪÉĻĖłŹö£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ“ęŌŚG1£Ø20£¬13£©”¢G2£Ø12£¬-3£©”¢G3£Ø0£¬3£©Ź¹µĆŅŌµćD”¢E”¢F”¢GĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µć![]() ŹĒ·“±ČĄżŗÆŹż
ŹĒ·“±ČĄżŗÆŹż![]() Ķ¼ĻńÉĻµÄČĪŅāŅ»µć£¬¹żµć
Ķ¼ĻńÉĻµÄČĪŅāŅ»µć£¬¹żµć![]() ×÷
×÷![]() ”Ī
”Ī![]() Öį£¬½»ĮķŅ»øö·“±ČĄżŗÆŹż
Öį£¬½»ĮķŅ»øö·“±ČĄżŗÆŹż![]() µÄĶ¼ĻńÓŚµć
µÄĶ¼ĻńÓŚµć![]() .
.
£Ø1£©Čō![]() £¬Ōņ
£¬Ōņ![]() ______ £»
______ £»
£Ø2£©µ±![]() Ź±£¬ Čōµć
Ź±£¬ Čōµć![]() µÄŗį×ų±źŹĒ1£¬Ēó
µÄŗį×ų±źŹĒ1£¬Ēó![]() µÄ¶ČŹż£»
µÄ¶ČŹż£»
£Ø3£©ČēĶ¼£¬Čō²»ĀŪµć![]() ŌŚŗĪ“¦£¬·“±ČĄżŗÆŹż
ŌŚŗĪ“¦£¬·“±ČĄżŗÆŹż![]() Ķ¼ĻńÉĻ×Ü“ęŌŚŅ»µć
Ķ¼ĻńÉĻ×Ü“ęŌŚŅ»µć![]() £¬Ź¹µĆĖıߊĪ
£¬Ź¹µĆĖıߊĪ![]() ĪŖĘ½ŠŠĖıߊĪ£¬Ēó
ĪŖĘ½ŠŠĖıߊĪ£¬Ēó![]() µÄÖµ.
µÄÖµ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬±ß³¤ĪŖ1µÄÕż·½ŠĪABCDµÄ¶Ō½ĒĻßAC”¢BDĻą½»ÓŚµćO£®ÓŠÖ±½Ē”ĻMPN£¬Ź¹Ö±½Ē¶„µćPÓėµćOÖŲŗĻ£¬Ö±½Ē±ßPM”¢PN·Ö±šÓėOA”¢OBÖŲŗĻ£¬Č»ŗóÄꏱÕėŠż×Ŗ”ĻMPN£¬Šż×Ŗ½ĒĪŖ¦Č£Ø0”ć£¼¦Č£¼90”ć£©£¬PM”¢PN·Ö±š½»AB”¢BCÓŚE”¢FĮ½µć£¬Į¬½ÓEF½»OBÓŚµćG£¬ŌņĻĀĮŠ½įĀŪÖŠÕżČ·µÄŹĒ £®
£Ø1£©EF=![]() OE£»£Ø2£©SĖıߊĪOEBF£ŗSÕż·½ŠĪABCD=1£ŗ4£»£Ø3£©BE+BF=
OE£»£Ø2£©SĖıߊĪOEBF£ŗSÕż·½ŠĪABCD=1£ŗ4£»£Ø3£©BE+BF=![]() OA£»£Ø4£©ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±”÷BEFÓė”÷COFµÄĆ껿֮ŗĶ×ī“óŹ±£¬AE=
OA£»£Ø4£©ŌŚŠż×Ŗ¹ż³ĢÖŠ£¬µ±”÷BEFÓė”÷COFµÄĆ껿֮ŗĶ×ī“óŹ±£¬AE=![]() £»£Ø5£©OGBD=AE2+CF2£®
£»£Ø5£©OGBD=AE2+CF2£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ2m©4Óė3m©1ŹĒĶ¬Ņ»øöÕżŹżµÄĮ½øöĘ½·½øł£¬ŌņmµÄÖµŹĒ£Ø””””£©
A. 0 B. 1 C. 2 D. 3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŌ²×¶µÄÄøĻß³¤5£¬µ×Ćę°ė¾¶ĪŖ3£¬ŌņŌ²×¶µÄ²ąĆ껿ĪŖ___________
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĆüĢā”°¶Ō½ĒĻßĻąµČµÄĖıߊĪŹĒ¾ŲŠĪ”±µÄÄęĆüĢāŹĒ_____________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠŌĖĖćÕżČ·µÄŹĒ£Ø £©
A.3a+2a=5a2
B.a6”Āa2=a3
C.£Ø©3a3£©2=9a6
D.£Øa+2£©2=a2+4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćP(3,£2018)ĖłŌŚĻóĻŽŹĒ(””””)
A. µŚŅ»ĻóĻŽB. µŚ¶žĻóĻŽC. µŚČżĻóĻŽD. µŚĖÄĻóĻŽ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠÓļ¾äÖŠÕżČ·µÄŹĒ£Ø £©
A. ²»Ļą½»µÄĮ½ĢõÖ±Ļß½Š×öĘ½ŠŠĻß B. ¹żŅ»µćÓŠĒŅÖ»ÓŠŅ»ĢõÖ±ĻßÓėŅŃÖŖÖ±ĻßĘ½ŠŠ
C. Į½Ö±ĻßĘ½ŠŠ£¬Ķ¬ÅŌÄŚ½ĒĻąµČ D. Į½ĢõÖ±Ļß±»µŚČżĢõÖ±ĻßĖł½Ų£¬Ķ¬Ī»½ĒĻąµČ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com