
【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.

【答案】(1)△ABD≌△EBD;(2)四边形AFED是菱形.
【解析】试题分析:(1)首先证明∠1=∠2.再由BA⊥AD,BE⊥CD可得∠BAD=∠BED=90°,然后再加上公共边BD=BD可得△ABD≌△EBD;
(2)首先证明四边形AFED是平行四边形,再有AD=ED,可得四边形AFED是菱形.
试题解析:证明:(1)如图,
∵AD∥BC,
∴∠1=∠DBC.
∵BC=DC,
∴∠2=∠DBC.
∴∠1=∠2.
∵BA⊥AD,BE⊥CD
∴∠BAD=∠BED=90°,
在△ABD和△EBD中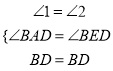 ,
,
∴△ABD≌△EBD(AAS);
(2)由(1)得,AD=ED,∠1=∠2.
∵EF∥DA,
∴∠1=∠3.
∴∠2=∠3.
∴EF=ED.
∴EF=AD.
∴四边形AFED是平行四边形.
又∵AD=ED,
∴四边形AFED是菱形.


科目:初中数学 来源: 题型:
【题目】某中学的部分学生参加该市中学生知识竞赛,小王同学统计了所有参赛同学的成绩,并且根据学过的知识绘制了统计图.请根据图中提供的信息回答问题:
(1)该校参加本竞赛的同学共_________人;
(2)若成绩在6分以上的(含6分)的同学获奖,则该校参赛同学的获奖率为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
(1)求这条抛物线对应的函数解析式;
(2)求直线AB对应的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中给出的信息,解答下列问题:
(1)放入一个小球水面升高 cm,放入一个大球水面升高 cm;
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广西省南宁市第22题)在南宁市地铁1号线某段工程建设中,甲队单独完成这项工程需要150天,甲队单独施工30天后增加乙队,两队又共同工作了15天,共完成总工程的![]() .
.
(1)求乙队单独完成这项工程需要多少天?
(2)为了加快工程进度,甲、乙两队各自提高工作效率,提高后乙队的工作效率是![]() ,甲队的工作效率是乙队的m倍(1≤m≤2),若两队合作40天完成剩余的工程,请写出a关于m的函数关系式,并求出乙队的最大工作效率是原来的几倍?
,甲队的工作效率是乙队的m倍(1≤m≤2),若两队合作40天完成剩余的工程,请写出a关于m的函数关系式,并求出乙队的最大工作效率是原来的几倍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com