
ΓΨΧβΡΩΓΩ≈ΉΈοœΏyΘΫ©¹x2+bx+c”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎBΉσ±ΏΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ°
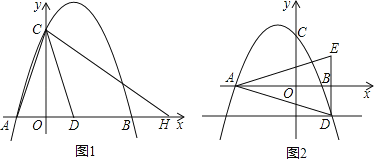
Θ®1Θ©»γΆΦ1Θ§“―÷ΣAΘ®©¹1Θ§0Θ©Θ§BΘ®3Θ§0Θ©Θ°
ΔΌ÷±Ϋ”–¥≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
ΔΎΒψH‘Ύx÷α…œΘ§DΘ®1Θ§0Θ©Θ§Ν§Ϋ”ACΘ§DCΘ§HCΘ§»τCDΤΫΖ÷ΓœACHΘ§«σΒψHΒΡΉχ±ξΘΜ
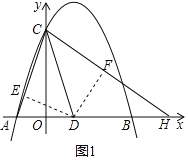
Θ®2Θ©»γΆΦ2Θ§÷±œΏyΘΫ©¹1”κ≈ΉΈοœΏyΘΫ©¹x2+bx+cΫΜ”ΎΒψDΘ§ΒψEΘ§DΙΊ”Ύx÷αΕ‘≥ΤΘ°
ΔΌ»τΒψD‘Ύ≈ΉΈοœΏΕ‘≥Τ÷αΒΡ”“≤ύΘ§«σ÷ΛΘΚDBΓΆAEΘΜ
ΔΎ»τΒψD‘Ύ≈ΉΈοœΏΕ‘≥Τ÷αΒΡΉσ≤ύΘ§«κ÷±Ϋ”≈–ΕœΘ§BD «Ζώ¥Ι÷±AEΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌyΘΫ©¹x2+2x+3ΘΜΔΎΒψHΒΡΉχ±ξΈΣΘ®![]() Θ§0Θ©ΘΜΘ®2Θ©ΔΌΦϊΫβΈωΘΜΔΎDBΓΆAE
Θ§0Θ©ΘΜΘ®2Θ©ΔΌΦϊΫβΈωΘΜΔΎDBΓΆAE
ΓΨΫβΈωΓΩ
Θ®1Θ©ΔΌ”Ο¥ΐΕ®œΒ ΐΖ®Ϋβ¥π±ψΩ…ΘΜ
ΔΎΙΐDΉςDEΓΆAC”ΎΒψEΘ§DFΓΆCH”ΎΒψFΘ§«σ≥ωDFΘ§…ηHΘ®mΘ§0Θ©Θ§‘Ό”…»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΝ–≥ωmΒΡΖΫ≥ΧΫχ––Ϋβ¥πΘΜ
Θ®2Θ©ΔΌ…ηDE”κx÷αΒΡΫΜΒψΈΣGΒψΘ§Ν§Ϋ”DBΘ§≤Δ―”≥ΛDB”κAEΫΜ”ΎΒψHΘ§‘Υ”Ο«σΚ· ΐΆΦœσΒΡΫΜΒψΉχ±ξΒΡΖΫΖ®«σ≥ωAΓΔBΘ§DΒψΉχ±ξΘ§«σΒΟDGΓΔBGΓΔAGΓΔEGΘ§‘Ό÷ΛΟςΓςDBGΓΉΓςAGE±ψΩ…ΒΟΫα¬έΘΜ
ΔΎΖ¬’’…œΟφΖΫΖ®±ψΩ…ΒΟΫα¬έΘ°
ΫβΘΚΘ®1Θ©ΔΌΑ―AΘ®©¹1Θ§0Θ©Θ§BΘ®3Θ§0Θ©¥ζ»κyΘΫ©¹x2+bx+cΘ§ΒΟ
![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚyΘΫ©¹x2+2x+3ΘΜ
ΔΎΙΐDΉςDEΓΆAC”ΎΒψEΘ§DFΓΆCH”ΎΒψFΘ§»γΆΦ1Θ§
ΓΏyΘΫ©¹x2+2x+3
ΓύCΘ®0Θ§3Θ©Θ§
ΓύOCΘΫ3Θ§
ΓΏAΘ®©¹1Θ§0Θ©Θ§BΘ®3Θ§0Θ©Θ§DΘ®1Θ§0Θ©Θ§
ΓύOAΘΫ1Θ§OBΘΫ3Θ§ODΘΫ1Θ§ADΘΫ2Θ§
Γύ![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓΏCDΤΫΖ÷ΓœACHΘ§
Γύ![]() Θ§
Θ§
…ηΒψHΒΡΉχ±ξΈΣΘ®mΘ§0Θ©Θ§‘ρDHΘΫm©¹1Θ§![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύmΘΫ©¹1Θ®…α»ΞΘ©Θ§Μρ![]() Θ§
Θ§
ΓύΒψHΒΡΉχ±ξΈΣΘ®![]() Θ§0Θ©ΘΜ
Θ§0Θ©ΘΜ
Θ®2Θ©ΔΌ…ηDE”κx÷αΒΡΫΜΒψΈΣGΒψΘ§Ν§Ϋ”DBΘ§≤Δ―”≥ΛDB”κAEΫΜ”ΎΒψHΘ§»γΆΦ2Θ§
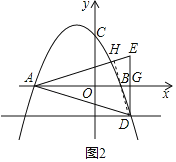
ΓΏ≈ΉΈοœΏyΘΫ©¹x2+bx+c”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎBΉσ±ΏΘ©Θ§
Γύ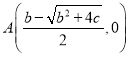 Θ§
Θ§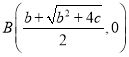 Θ§
Θ§
ΓΏ÷±œΏyΘΫ©¹1”κ≈ΉΈοœΏyΘΫ©¹x2+bx+cΫΜ”ΎΒψDΘ§ΒψD‘Ύ≈ΉΈοœΏΕ‘≥Τ÷αΒΡ”“≤ύΘ§
ΓύDΒψΒΡΉχ±ξΈΣ Θ§
Θ§
ΓΏΒψEΘ§DΙΊ”Ύx÷αΕ‘≥ΤΘ§
Γύ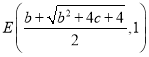 Θ§DGΘΫEGΘΫ1Θ§
Θ§DGΘΫEGΘΫ1Θ§
Γύ![]() Θ§
Θ§
![]()
Γύ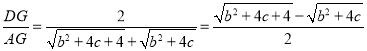 Θ§
Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓΏΓœDGBΘΫΓœAGEΘΫ90ΓψΘ§
ΓύΓςDGBΓΉΓςAGEΘ§
ΓύΓœBDGΘΫΓœEAGΘ§
ΓΏΓœEAG+ΓœAEGΘΫ90ΓψΘ§
ΓύΓœBDG+ΓœAEGΘΫ90ΓψΘ§
ΓύΓœDHEΘΫ90ΓψΘ§
ΓύDBΓΆAEΘΜ
ΔΎBDΓΆAEΘ°»γΆΦ3Θ§
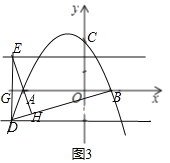
ΓΏ≈ΉΈοœΏyΘΫ©¹x2+bx+c”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎBΉσ±ΏΘ©Θ§
Γύ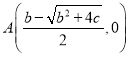 Θ§
Θ§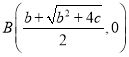 Θ§
Θ§
ΓΏ÷±œΏyΘΫ©¹1”κ≈ΉΈοœΏyΘΫ©¹x2+bx+cΫΜ”ΎΒψDΘ§ΒψD‘Ύ≈ΉΈοœΏΕ‘≥Τ÷αΒΡΉσ≤ύΘ§
ΓύDΒψΒΡΉχ±ξΈΣ Θ§
Θ§
ΓΏΒψEΘ§DΙΊ”Ύx÷αΕ‘≥ΤΘ§
Γύ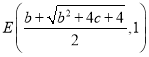 Θ§DGΘΫEGΘΫ1Θ§
Θ§DGΘΫEGΘΫ1Θ§
Γύ![]() Θ§
Θ§
![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓΏΓœDGBΘΫΓœAGFΘΫ90ΓψΘ§
ΓύΓςDGBΓΉΓςAGEΘ§
ΓύΓœBDGΘΫΓœEAGΘ§
ΓΏΓœEAG+ΓœAEGΘΫ90ΓψΘ§
ΓύΓœBDG+ΓœAEGΘΫ90ΓψΘ§
ΓύΓœDHEΘΫ90ΓψΘ§
ΓύDBΓΆAEΘ°
Ι ¥πΑΗ «ΘΚΘ®1Θ©ΔΌyΘΫ©¹x2+2x+3ΘΜΔΎΒψHΒΡΉχ±ξΈΣΘ®![]() Θ§0Θ©ΘΜΘ®2Θ©ΔΌΦϊΫβΈωΘΜΔΎDBΓΆAE
Θ§0Θ©ΘΜΘ®2Θ©ΔΌΦϊΫβΈωΘΜΔΎDBΓΆAE



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
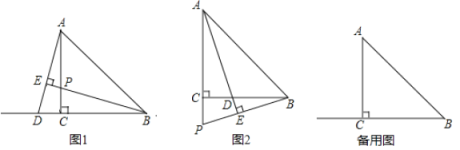
ΓΨΧβΡΩΓΩ»γΆΦ1ΚΆΆΦ2Θ§‘ΎΓςABC÷–Θ§ABΘΫ13Θ§BCΘΫ14Θ§![]() .
.
ΧΫΨΩΘΚ»γΆΦ1Θ§AHΓΆBC”ΎΒψHΘ§‘ρAHΘΫ___Θ§ACΘΫ___Θ§ΓςABCΒΡΟφΜΐ![]() ΘΫ___.
ΘΫ___.
ΆΊ’ΙΘΚ»γΆΦ2Θ§ΒψD‘ΎAC…œΘ®Ω…”κΒψAΓΔC÷ΊΚœΘ©Θ§Ζ÷±πΙΐΒψAΓΔCΉς÷±œΏBDΒΡ¥ΙœΏΘ§¥ΙΉψΈΣEΓΔFΘ§…ηBDΘΫxΘ§AEΘΫmΘ§CFΘΫnΘ§Θ®Β±ΒψD”κA÷ΊΚœ ±Θ§Έ“Ο«»œΈΣ![]() ΘΫ0Θ©.
ΘΫ0Θ©.
Θ®1Θ©”ΟΚ§xΓΔmΜρnΒΡ¥ζ ΐ Ϋ±μ Ψ![]() ΦΑ
ΦΑ![]() ΘΜ
ΘΜ
Θ®2Θ©«σ(m+n)”κxΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ«σ(m+n)ΒΡΉν¥σ÷ΒΚΆΉν–Γ÷ΒΘΜ
Θ®3Θ©Ε‘ΗχΕ®ΒΡ“ΜΗωx÷ΒΘ§”– ±÷ΜΡή»ΖΕ®Έ®“ΜΒΡΒψDΘ§÷Η≥ω’β―υΒΡxΒΡ»Γ÷ΒΖΕΈß.
ΖΔœ÷ΘΚ«κΡψ»ΖΕ®“ΜΧθ÷±œΏΘ§ ΙΒΟAΓΔBΓΔC»ΐΒψΒΫ’βΧθ÷±œΏΒΡΨύάκ÷°ΚΆΉν–ΓΘ®≤Μ±Ί–¥≥ωΙΐ≥ΧΘ©Θ§≤Δ–¥≥ω’βΗωΉν–Γ÷Β.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§≈ΉΈοœΏyΘΫ-![]() x2+
x2+![]() x+
x+![]() ”κx÷αΫΜ”ΎAΓΔBΝΫΒψ(ΒψA‘ΎΒψBΒΡΉσ≤ύ)Θ§ΫΜy÷α”ΎΒψCΘ°ΫΪ÷±œΏAC“‘ΒψAΈΣ–ΐΉΣ÷––ΡΘ§Υ≥ ±’κ–ΐΉΣ90ΓψΘ§ΫΜy÷α”ΎΒψDΘ§ΫΜ£¹ΈοœΏ”ΎΝμ“ΜΒψEΘ°
”κx÷αΫΜ”ΎAΓΔBΝΫΒψ(ΒψA‘ΎΒψBΒΡΉσ≤ύ)Θ§ΫΜy÷α”ΎΒψCΘ°ΫΪ÷±œΏAC“‘ΒψAΈΣ–ΐΉΣ÷––ΡΘ§Υ≥ ±’κ–ΐΉΣ90ΓψΘ§ΫΜy÷α”ΎΒψDΘ§ΫΜ£¹ΈοœΏ”ΎΝμ“ΜΒψEΘ°
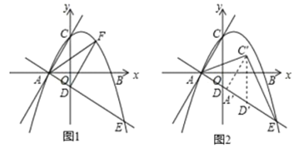
(1)«σ÷±œΏAEΒΡΫβΈω ΫΘΜ
(2)ΒψF «ΒΎ“ΜœσœόΡΎ≈ΉΈοœΏ…œ“ΜΒψΘ§Β±ΓςFADΒΡΟφΜΐΉν¥σ ±Θ§«σ≥ω¥Υ ±ΒψFΒΡΉχ±ξΘΜ
(3)»γΆΦ2Θ§ΫΪΓςACD―Ί…δœΏAEΖΫœρ“‘ΟΩΟκ![]() ΗωΒΞΈΜΒΡΥΌΕ»ΤΫ“ΤΘ§Φ«ΤΫ“ΤΚσΒΡΓςACDΈΣΓςAΓδCΓδDΓδΘ§ΤΫ“Τ ±ΦδΈΣtΟκΘ§Β±ΓςACΓδEΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§«σtΒΡ÷ΒΘ°
ΗωΒΞΈΜΒΡΥΌΕ»ΤΫ“ΤΘ§Φ«ΤΫ“ΤΚσΒΡΓςACDΈΣΓςAΓδCΓδDΓδΘ§ΤΫ“Τ ±ΦδΈΣtΟκΘ§Β±ΓςACΓδEΈΣΒ»―ϋ»ΐΫ«–Έ ±Θ§«σtΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§Βψ
Θ§Βψ![]() «…δœΏ
«…δœΏ![]() …œ“ΜΕ·ΒψΘ§ΙΐΒψ
…œ“ΜΕ·ΒψΘ§ΙΐΒψ![]() Ής
Ής![]() Θ§¥ΙΉψΈΣΒψ
Θ§¥ΙΉψΈΣΒψ![]() Θ§ΫΜ÷±œΏ
Θ§ΫΜ÷±œΏ![]() ”ΎΒψ
”ΎΒψ![]() Θ°
Θ°
Θ®Έ ΧβΖΔœ÷Θ©Θ®1Θ©»γΆΦ1Θ§»τΒψ![]() ‘Ύ
‘Ύ![]() ΒΡ―”≥ΛœΏ…œΘ§ ‘≤¬œκ
ΒΡ―”≥ΛœΏ…œΘ§ ‘≤¬œκ![]() Θ§
Θ§![]() Θ§
Θ§![]() ÷°ΦδΒΡ ΐΝΩΙΊœΒΈΣ_______ΘΜ
÷°ΦδΒΡ ΐΝΩΙΊœΒΈΣ_______ΘΜ
Θ®άύ±»ΧΫΨΩΘ©Θ®2Θ©»γΆΦ2Θ§»τΒψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§ ‘≤¬œκ
…œΘ§ ‘≤¬œκ![]() Θ§
Θ§![]() Θ§
Θ§![]() ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®ΆΊ’Ι”Π”ΟΘ©Θ®3Θ©Β±Βψ![]() ΈΣ
ΈΣ![]() ΒΡ÷–Βψ ±Θ§÷±Ϋ”–¥≥ωœΏΕΈ
ΒΡ÷–Βψ ±Θ§÷±Ϋ”–¥≥ωœΏΕΈ![]() ΒΡ≥ΛΕ»Θ°
ΒΡ≥ΛΕ»Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥Ά§―ßΫχ––…γΜαΒς≤ιΘ§ΥφΜζ≥ι≤ιΝΥΡ≥Ηω–Γ«χΒΡ200ΜßΦ“ΆΞΒΡΡξ ’»κΘ§≤ΔΜφ÷Τ≥…Ά≥ΦΤΆΦΘ®»γΆΦΘ©Θ°«κΡψΗυΨίΆ≥ΦΤΆΦΗχ≥ωΒΡ–≈œΔΜΊ¥πΘΚ
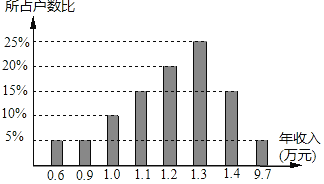
Θ®1Θ©―υ±Ψ ΐΨίΒΡ÷–ΈΜ ΐ «_____Θ§÷Ύ ΐ «_____ΘΜ
Θ®2Θ©’β200ΜßΦ“ΆΞΒΡΤΫΨυΡξ ’»κΈΣ_____Άρ‘ΣΘΜ
Θ®3Θ©‘ΎΤΫΨυ ΐΓΔ÷–ΈΜ ΐΝΫ ΐ÷–Θ§_____ΗϋΡήΖ¥”≥’βΗω–Γ«χΦ“ΆΞΒΡΡξ ’»κΥ°ΤΫΘ°
Θ®4Θ©»γΙϊΗΟ–Γ«χ”–1200ΜßΉΓΜßΘ§«κΡψΗυΨί≥ι―υΒς≤ιΒΡΫαΙϊΙάΦΤΗΟ–Γ«χ”–_____ΜßΦ“ΆΞΒΡΡξ ’»κΒΆ”Ύ1.3Άρ‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
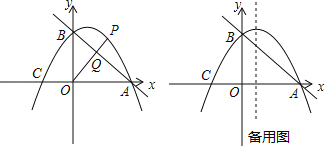
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏy=©¹![]() x+3”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ°≈ΉΈοœΏy=©¹
x+3”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ°≈ΉΈοœΏy=©¹![]() x2+bx+cΨ≠ΙΐAΓΔBΝΫΒψΘ§”κx÷αΒΡΝμ“ΜΗωΫΜΒψΈΣCΘ°
x2+bx+cΨ≠ΙΐAΓΔBΝΫΒψΘ§”κx÷αΒΡΝμ“ΜΗωΫΜΒψΈΣCΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΒψP «ΒΎ“Μœσœό≈ΉΈοœΏ…œΒΡΒψΘ§Ν§Ϋ”OPΫΜ÷±œΏAB”ΎΒψQΘ°…ηΒψPΒΡΚαΉχ±ξΈΣmΘ§PQ”κOQΒΡ±»÷ΒΈΣyΘ§«σy”κmΒΡΙΊœΒ ΫΘ§≤Δ«σ≥ωPQ”κOQΒΡ±»÷ΒΒΡΉν¥σ÷ΒΘΜ
Θ®3Θ©ΒψD «≈ΉΈοœΏΕ‘≥Τ÷α…œΒΡ“ΜΕ·ΒψΘ§Ν§Ϋ”ODΓΔCDΘ§…ηΓςODCΆβΫ”‘≤ΒΡ‘≤–ΡΈΣMΘ§Β±sinΓœODCΒΡ÷ΒΉν¥σ ±Θ§«σΒψMΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–Έ![]() ΒΡ
ΒΡ![]() ±Ώ…œ»Γ“ΜΒψ
±Ώ…œ»Γ“ΜΒψ![]() ΫΪ
ΫΪ![]() ―Ί
―Ί![]() ’έΒΰΘ§ΕΞΒψ
’έΒΰΘ§ΕΞΒψ![]() ’ΐΚΟ¬δ‘Ύ
’ΐΚΟ¬δ‘Ύ![]() ±ΏΒΡ÷–Βψ
±ΏΒΡ÷–Βψ![]() …œΘ§
…œΘ§![]() …η
…η![]() Θ°
Θ°
Θ®1Θ©÷±Ϋ”–¥≥ω![]() ΒΡ÷ΒΚΆ
ΒΡ÷ΒΚΆ![]() ΒΡΕ» ΐΘΜ
ΒΡΕ» ΐΘΜ
Θ®2Θ©«σ÷ΛΘΚ÷±œΏ![]() «“‘
«“‘![]() ΈΣ÷±ΨΕΒΡ
ΈΣ÷±ΨΕΒΡ![]() ΒΡ«–œΏΘΜ
ΒΡ«–œΏΘΜ
Θ®3Θ©Ν§Ϋ”![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() «σ
«σ![]() ΒΡ±Ώ
ΒΡ±Ώ![]() …œΒΡΗΏΘ°
…œΒΡΗΏΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
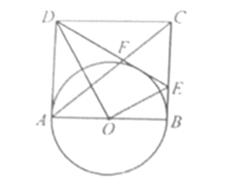
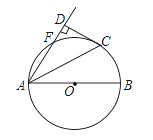
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§ΒψFΓΔC‘ΎΓ―O…œ«“![]() Θ§ Ν§Ϋ”ACΓΔAFΘ§ΙΐΒψCΉςCDΓΆAFΫΜAFΒΡ―”≥ΛœΏ”ΎΒψDΘ°
Θ§ Ν§Ϋ”ACΓΔAFΘ§ΙΐΒψCΉςCDΓΆAFΫΜAFΒΡ―”≥ΛœΏ”ΎΒψDΘ°
Θ®1Θ©«σ÷ΛΘΚCD «Γ―OΒΡ«–œΏΘΜ
Θ®2Θ©»τ![]() Θ§ CD=4Θ§«σΓ―OΒΡΑκΨΕΘ°
Θ§ CD=4Θ§«σΓ―OΒΡΑκΨΕΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
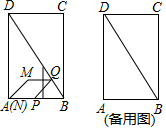
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§AB=2cmΘ§ΓœADB=30ΓψΘ°PΘ§QΝΫΒψΖ÷±π¥”AΘ§BΆ§ ±≥ωΖΔΘ§ΒψP―Ί’έœΏAB©¹BC‘ΥΕ·Θ§‘ΎAB…œΒΡΥΌΕ» «2cm/sΘ§‘ΎBC…œΒΡΥΌΕ» «2![]() cm/sΘΜΒψQ‘ΎBD…œ“‘2cm/sΒΡΥΌΕ»œρ÷’ΒψD‘ΥΕ·Θ§ΙΐΒψPΉςPNΓΆADΘ§¥ΙΉψΈΣΒψNΘ°Ν§Ϋ”PQΘ§“‘PQΘ§PNΈΣΝΎ±ΏΉςPQMNΘ°…η‘ΥΕ·ΒΡ ±ΦδΈΣxΘ®sΘ©Θ§PQMN”κΨΊ–ΈABCD÷ΊΒΰ≤ΩΖ÷ΒΡΆΦ–ΈΟφΜΐΈΣyΘ®cm2Θ©
cm/sΘΜΒψQ‘ΎBD…œ“‘2cm/sΒΡΥΌΕ»œρ÷’ΒψD‘ΥΕ·Θ§ΙΐΒψPΉςPNΓΆADΘ§¥ΙΉψΈΣΒψNΘ°Ν§Ϋ”PQΘ§“‘PQΘ§PNΈΣΝΎ±ΏΉςPQMNΘ°…η‘ΥΕ·ΒΡ ±ΦδΈΣxΘ®sΘ©Θ§PQMN”κΨΊ–ΈABCD÷ΊΒΰ≤ΩΖ÷ΒΡΆΦ–ΈΟφΜΐΈΣyΘ®cm2Θ©
Θ®1Θ©Β±PQΓΆAB ±Θ§xΒ»”ΎΕύ…ΌΘΜ
Θ®2Θ©«σyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘ§≤Δ–¥≥ωxΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©÷±œΏAMΫΪΨΊ–ΈABCDΒΡΟφΜΐΖ÷≥…1ΘΚ3ΝΫ≤ΩΖ÷ ±Θ§÷±Ϋ”–¥≥ωxΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com