
 如图,已知AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC,且BC=2
如图,已知AB是⊙O的直径,PA切⊙O于点A,OP交⊙O于点C,连接BC,且BC=2| 3 |
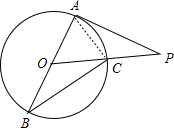 解:连结AC,如图,
解:连结AC,如图,| BC |
| AB |
2
| ||||
|


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由.
如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
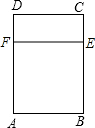 现有铝合金窗框材料8米,准备用它做一个如图所示的长方形窗架(窗架宽度AB必须小于窗架的高度BC).已知窗台距离房屋天花板2.2米.设AB为x米,窗架的总面积为S平方米.试写出S与x的函数关系式,并求自变量x的取值范围.
现有铝合金窗框材料8米,准备用它做一个如图所示的长方形窗架(窗架宽度AB必须小于窗架的高度BC).已知窗台距离房屋天花板2.2米.设AB为x米,窗架的总面积为S平方米.试写出S与x的函数关系式,并求自变量x的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com