
【题目】如图,△ABC内接于⊙O,AB=8,AC=4,D是AB边上一点,P是优弧![]() 的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.

【答案】当BD=4时,△PAD是以AD为底边的等腰三角形.理由见解析.
【解析】
解:当BD=4时,△PAD是以AD为底边的等腰三角形。理由如下:
∵P是优弧![]() 的中点,∴
的中点,∴![]() 。∴PB=PC。
。∴PB=PC。
若△PAD是以AD为底边的等腰三角形,则PA=PD。
又∵∠PAD=∠PCB,∴△PAD∽△PCB。∴∠DPA=∠BPC。∴∠BPD=∠CPA。
在△PBD与△PCA中,∵PB=PC,∠BPD=∠CPA,PD="PA" ,∴△PBD≌△PCA(SAS)。
∴BD=AC=4。
由于以上结论,反之也成立,
∴当BD=4时,△PAD是以AD为底边的等腰三角形。
根据等弧对等弦以及全等和相似三角形的判定与性质进行求解。


科目:初中数学 来源: 题型:
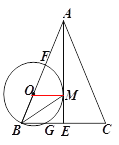
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.

(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,是图中阴影部分的面积为( )

A. ![]() π﹣6 B.
π﹣6 B. ![]() π C.
π C. ![]() π﹣3 D.
π﹣3 D. ![]() +π
+π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDE都是等边三角形,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AFB=60°;③BF=AH;④△ECF≌△DCG;⑤连CG,则∠BGC=∠DGC.其中正确的个数是()

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com