
已知:△ABC中,∠A=90°,AB=AC,D为BC的中点,
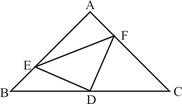
(1)如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?证明你的结论.
(1)连接AD,由AD是等腰直角三角形ABC底边上的中线,可得∠CAD=∠BAD=45°,AD=BD=CD,而即可得到∠B=∠DAF,再有BE=AF,AD=BD,即可证得△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即可证得结论;(2)仍为等腰直角三角形
【解析】
试题分析:(1)连接AD,由AD是等腰直角三角形ABC底边上的中线,可得∠CAD=∠BAD=45°,AD=BD=CD,而即可得到∠B=∠DAF,再有BE=AF,AD=BD,即可证得△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即可证得结论;
(2)先由∠DBE=180°-45°=135°,∠DAF=90°+45°=135°,可得∠DAF=∠DBE,再结合两组对边对应相等,即可证得△BED≌△AFD从而证得结论.
① 连结AD,
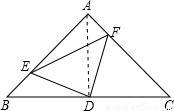
∵ ,∠BAC=90°,
,∠BAC=90°, 为BC的中点
为BC的中点
∴AD⊥BC,BD=AD
∴∠B=∠DAC=45°
又∵BE=AF
∴△BDE≌△ADF(SAS)
∴ED=FD,∠BDE=∠ADF
∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°
∴△DEF为等腰直角三角形;
②若E,F分别是AB,CA延长线上的点,如图所示,连结AD
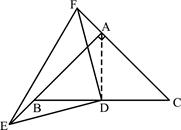
∵AB=AC,∠BAC=90°,D为BC的中点
∴AD=BD,AD⊥BC
∴∠DAC=∠ABD=45°
∴∠DAF=∠DBE=135°
又AF=BE
∴△DAF≌△DBE(SAS)
∴FD=ED,∠FDA=∠EDB
∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°
∴△DEF仍为等腰直角三角形.
考点:本题考查的是等腰直角三角形的性质,全等三角形的判定和性质
点评:解答本题的关键是熟练掌握等腰直角三角形底边上的中线平分顶角,并且等于底边的一半.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 3 |
| 4 |
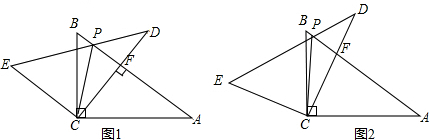
| 25 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.
8、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、C、E在同一直线上,则下列结论:①AB=AC;②∠CAE=∠E;③AB+BD=DE;④∠BAC=∠ACB.正确的个数有( )个.查看答案和解析>>
科目:初中数学 来源: 题型:
 外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,
外切于点D,若AC和BC边的长是关于x的方程x2-(AB+4)x+4AB+8=0的两根,且25BC•sinA=9AB,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com