
【题目】如图,在△ABC中,B、C两点恰好在反比例函数y= ![]() (k>0)第一象限的图象上,且BC=
(k>0)第一象限的图象上,且BC= ![]() ,S△ABC=
,S△ABC= ![]() ,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为 .
,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为 . 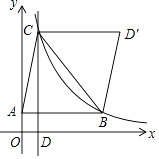
科目:初中数学 来源: 题型:
【题目】解方程组:①![]() ②
②![]() ③
③![]() ④
④![]() ,比较适宜的方法是( )
,比较适宜的方法是( )
A.①②用代入法,③④用加减法B.①③用代入法,②④用加减法
C.②③用代入法,①④用加减法D.②④用代入法,①③用加减法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园,诵读经典”活动,随机抽查了部分学生,对他们每天的课外阅读时长进行统计,并将结果分为四类:设每天阅读时长为t分钟,当0<t≤20时记为A类,当20<t≤40时记为B类,当40<t≤60时记为C类,当t>60时记为D类,收集的数据绘制成如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题:

(1)这次共抽取了 名学生进行调查统计,扇形统计图中的D类所对应的扇形圆心角为 °;
(2)将条形统计图补充完整;
(3)若该校共有2000名学生,请估计该校每天阅读时长超过40分钟的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【发现证明】
如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系.
小聪把△ABE绕点A逆时针旋转90°至△ADG,通过证明△AEF≌△AGF;从而发现并证明了EF=BE+FD.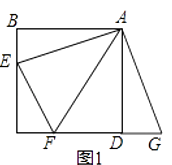
(1)【类比引申】如图2,点E、F分别在正方形ABCD的边CB、CD的延长线上,∠EAF=45°,连接EF,请根据小聪的发现给你的启示写出EF、BE、DF之间的数量关系,并证明;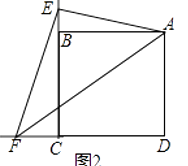
(2)【联想拓展】如图4,如图,∠BAC=90°,AB=AC,点E、F在边BC上,且∠EAF=45°,若BE=3,EF=5,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小芸设计的“作三角形一边上的高”的尺规作图过程.
已知:△ABC.
求作:△ABC的边BC上的高AD.
作法:①以点A为圆心,适当长为半径画弧,
交直线BC于点M,N;
②分别以点M,N为圆心,以大于![]() MN的长为半径画弧,两弧相交于点P;
MN的长为半径画弧,两弧相交于点P;
③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.
根据小芸设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵AM= ,MP= ,
∴AP是线段MN的垂直平分线.( )(填推理的依据)
∴AD⊥BC于D,即线段AD为△ABC的边BC上的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )

A. ①② B. ①③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,小明和小颖相约到乐山大佛景区参观.小明乘私家车从成都出发1小时后,小颖乘坐高铁从成都出发,先到乐山高铁站,然后转乘出租车到乐山大佛景区(换车时间忽略不计),两人恰好同时到达景区.他们离开成都的距离y(千米)与时间t(小时)的关系如图所示,请结合图象解决下面问题.
(1)高铁的平均速度是每小时多少千米?
(2)当小颖到达乐山高铁站时,小明距离乐山大佛景区还有多少千米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com