
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC绕点B顺时针旋转90°得到△A′BC′,请画出△A′BC′.
(2)求BA边旋转到BA′位置时所扫过图形的面积.
 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AC∥DF,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连结CF,再找出CF的中点O,然后连结EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.

以下是他的想法,请你填上根据.小华是这样想的:
因为CF和BE相交于点O,
根据 得出∠COB=∠EOF;
而O是CF的中点,那么CO=FO,又已知 EO=BO,
根据 得出△COB≌△FOE,
根据 得出BC=EF,
根据 得出∠BCO=∠F,
既然∠BCO=∠F,根据 出AB∥DF,
既然AB∥DF,根据 得出∠ACE和∠DEC互补.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信思给出下列说法,其中错误的是( )

A. 每分钟进水5升
B. 每分钟放水1.25升
C. 若12分钟后只放水,不进水,还要8分钟可以把水放完
D. 若从一开始进出水管同时打开需要24分钟可以将容器灌满
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨华与季红用5张同样规格的硬纸片做拼图游戏,正面如图1所示,背面完全一样,将它们背面朝上搅匀后,同时抽出两张.规则如下:当两张硬纸片上的图形可拼成电灯或小人时,杨华得1分;当两张硬纸片上的图形可拼成房子或小山时,季红得1分(如图2).问题:游戏规则对双方公平吗?请说明理由;若你认为不公平,如何修改游戏规则才能使游戏对双方公平?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,点E在BC上,BD=BE.
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明.你添加的条件是 .
(2)根据你添加的条件,再写出图中的一对全等三角形 .(只要求写出一对全等三角形,不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.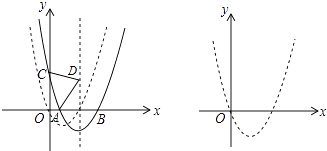
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△ PAC为等边三角形,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M的表示的数为________________.
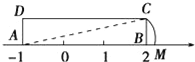
【答案】![]()
【解析】AC=AM=![]() =
=![]() ,∴AM=
,∴AM=![]()
【题型】填空题
【结束】
11
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,b,定义运算“*”:a*b=a2-ab(a≤b); a*b=b2-ab(a>b),关于x的方程(2x-1)*(x-1)=m 恰好有三个不相等的实数根,则m的取值范围是( )
A.m> ![]()
B. ![]()
C. ![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com