
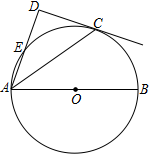
 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.分析 (1)连接OC,根据切线的性质和已知求出OC∥AD,求出∠OCA=∠CAO=∠DAC,即可得出答案;
(2)连接BE、BC、OC,BE交AC于F交OC于H,根据cos∠CAD=$\frac{4}{5}$=$\frac{AD}{AC}$,设AD=4a,AC=5a,则DC=EH=HB=3a,根据cos∠CAB=$\frac{4}{5}$=$\frac{AC}{AB}$,求出AB、BC,再根据勾股定理求出CH,由此即可解决问题;
解答 (1)证明:连接OC,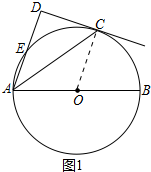
∵CD是⊙O的切线,
∴CD⊥OC,
又∵CD⊥AD,
∴AD∥OC,
∴∠CAD=∠ACO,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠CAD=∠CAO,
即AC平分∠DAB;
(2)解:连接BE、BC、OC,BE交AC于F交OC于H.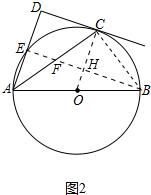
∵AB是直径,
∴∠AEB=∠DEH=∠D=∠DCH=90°,
∴四边形DEHC是矩形,
∴∠EHC=90°即OC⊥EB,
∴DC=EH=HB,DE=HC,
∵cos∠CAD=$\frac{4}{5}$=$\frac{AD}{AC}$,设AD=4a,AC=5a,则DC=EH=HB=3a,
∵cos∠CAB=$\frac{4}{5}$=$\frac{AC}{AB}$,
∴AB=$\frac{25}{4}$a,BC=$\frac{15}{4}$a,
在RT△CHB中,CH=$\sqrt{C{B}^{2}-B{H}^{2}}$=$\frac{9}{4}$a,
∴DE=CH=$\frac{9}{4}$a,AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\frac{7}{4}$a,
∵EF∥CD,
∴$\frac{AF}{FC}$=$\frac{AE}{ED}$=$\frac{7}{9}$.
点评 本题考查了切线的性质,平行线的性质和判定,勾股定理,圆周角定理,圆心角、弧、弦之间的关系的应用,能灵活运用知识点进行推理是解此题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,AC是⊙O的弦,OF⊥AC于点F,延长OF,与过点A的切线交于点P,若∠P=30°,AP=$\sqrt{3}$,则OF的值是( )
如图,AC是⊙O的弦,OF⊥AC于点F,延长OF,与过点A的切线交于点P,若∠P=30°,AP=$\sqrt{3}$,则OF的值是( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{1}{3}$ | C. | 3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
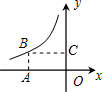 如图,矩形OABC上,点A、C分别在x、y轴上,点B在反比例y=$\frac{k}{x}$位于第二象限的图象上,矩形面积为6,则k的值是( )
如图,矩形OABC上,点A、C分别在x、y轴上,点B在反比例y=$\frac{k}{x}$位于第二象限的图象上,矩形面积为6,则k的值是( )| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25.
如图,某数学兴趣小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为25.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}与\sqrt{3}$ | B. | $\sqrt{12}与\sqrt{27}$ | C. | $\sqrt{a}与\sqrt{b}$ | D. | $\sqrt{a}与\sqrt{2a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 运动鞋型号的平均数 | B. | 运动鞋型号的众数 | ||
| C. | 运动鞋型号的中位数 | D. | 运动鞋型号的极差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com