
分析 利用因式分解法解方程易得x1=-$\frac{1}{3}$,x2=$\frac{m}{m-2}$;则x=$\frac{m}{m-2}$为正整数,先变形为1+$\frac{2}{m-2}$,然后利用整数的整除性可确定m的值即可.
解答 解:3(m-2)x2-2(m+1)x-m=0
(3x+1)[(m-2)x-m]=0
解得x1=-$\frac{1}{3}$,x2=$\frac{m}{m-2}$;
∵关于x的一元二次方程3(m-2)x2-2(m+1)x-m=0有正整数根,
∴x=$\frac{m}{m-2}$=1+$\frac{2}{m-2}$为正整数,
∴m-2=1或2时,x=$\frac{m}{m-2}$为正整数,则m=3或4.
即所有满足条件的整数m的值为3或4.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
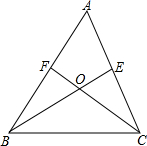 如图,在△ABC中,BE平分∠ABC,F是AB边上一点,CF交BE于点O,∠BOC=90°+$\frac{1}{2}$∠A,请你用推理的方法说明CF平分∠ACB.
如图,在△ABC中,BE平分∠ABC,F是AB边上一点,CF交BE于点O,∠BOC=90°+$\frac{1}{2}$∠A,请你用推理的方法说明CF平分∠ACB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-5) | B. | (-2,5) | C. | (2,-5) | D. | (2,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是一个边长为a的正方形.两条对角线AC与BD相交于O.观察此图并回答下面问题:
如图是一个边长为a的正方形.两条对角线AC与BD相交于O.观察此图并回答下面问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )
如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE是AB的垂直平分线,DE=$\frac{1}{2}$BD,DE=1.5cm,则AC等于( )| A. | 3cm | B. | 7.5cm | C. | 6cm | D. | 4.5cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com