
 某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图
某公司共有A、B、C三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图| 部门 | 员工人数 | 每人所创的年利润/万元 |
| A | 5 | 10 |
| B | b | 8 |
| C | c | 5 |
分析 (1)①根据扇形圆心角的度数=部分占总体的百分比×360°进行计算即可;②先求得A部门的员工人数所占的百分比,进而得到各部门的员工总人数,据此可得B,C部门的人数;
(2)根据总利润除以总人数,即可得到这个公司平均每人所创年利润.
解答 解:(1)①在扇形图中,C部门所对应的圆心角的度数为:360°×30%=108°;
②A部门的员工人数所占的百分比为:1-30%-45%=25%,
各部门的员工总人数为:5÷25%=20(人),
∴b=20×45%=9,c=20×30%=6,
故答案为:108°,9,6;
(2)这个公司平均每人所创年利润为:$\frac{5×10+9×8+6×5}{20}$=7.6(万元).
点评 本题主要考查了扇形统计图以及平均数的计算,解题时注意:通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系,用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
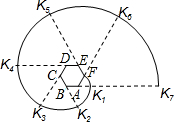 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1,弧K1K2,弧K2K3,弧K3K4,弧K4K5,弧K5K6,…的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1,L2,L3,L4,L5,L6,….当AB=1时,L2016等于( )| A. | $\frac{2016π}{2}$ | B. | $\frac{2016π}{3}$ | C. | $\frac{2016π}{4}$ | D. | $\frac{2016π}{6}$. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
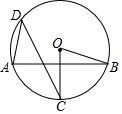 如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=35度.
如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=35度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com