
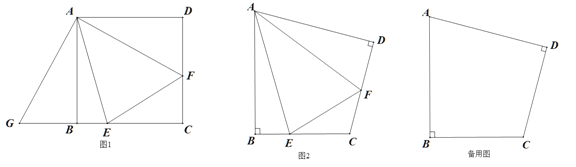
【题目】(1)如图1,在正方形ABCD中,E、F分别是边BC、CD上的点,且∠EAF=45°,把△ADF绕着点A顺时针旋转90°得到△ABG,请直接写出图中所有的全等三角形;
(2)在四边形ABCD中,AB=AD,∠B=∠D=90°.
①如图2,若E、F分别是边BC、CD上的点,且2∠EAF=∠BAD,求证:EF=BE+DF;
②若E、F分别是边BC、CD延长线上的点,且2∠EAF=∠BAD,①中的结论是否仍然成立?请说明理由
【答案】(1)△ADF≌△ABG、△AEF≌△AEG;(2)①证明见解析;②不成立;理由见解析;
【解析】
(1)由旋转的性质易得△ADF≌△ABG、△AEF≌△AEG;
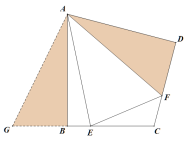
(2)①如图,将△ADF绕着点A顺时针旋转,使AD与AB重合,易证△ADF≌△ABG,故∠DAF=∠BAG,AF=AG,DF=BG,由2∠EAF=∠BAD得∠EAF=∠EAG,从而得△AEF≌△AEG,易得证;
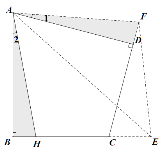
②不成立.如图,将△ADF绕着点A顺时针旋转,使AD与AB重合,得△ABH,可证得△AEF≌△AEH,从而得出EF=BE-DF.
(1)△ADF≌△ABG、△AEF≌△AEG;
(2)①如图,将△ADF绕着点A顺时针旋转,使AD与AB重合,得△ABG,
∵AB=AD,∠ABC=∠D=![]() ,
,
∴∠ABC+∠ABG=![]() 即∠GBC=
即∠GBC=![]() ,
,
易得△ADF≌△ABG,
∴∠DAF=∠BAG,AF=AG,DF=BG,
∵2∠EAF=∠BAD,
∴∠EAF=∠BAE+∠DAF=∠BAE+∠BAG=∠EAG,
∵AE=AE,
∴△AEF≌△AEG,
∴EF=EG=BE+BG=BE+DF,
即EF=BE+DF.
②不成立
理由如下:如图,将△ADF绕着点A顺时针旋转,使AD与AB重合,得△ABH,
∵AB=AD,∠B=∠ADC=∠ADF=![]()
∴点H在BC上,易得AF=AH,BH=DF,∠1=∠2
∴∠EAF=∠EAD+∠1=∠EAD+∠2,
∵2∠EAF=∠BAD=∠EAD+∠2+∠EAH,
∴∠EAF=∠EAH,
又∵AE=AE,
∴△AEF≌△AEH,
∴EF=EH=BE-BH=BE-DF,即EF=BE-DF,
∴①中的结论不成立.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=∠C,点P在边AB上. 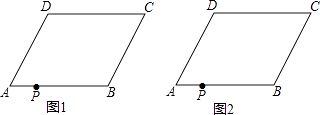
(1)判断四边形ABCD的形状并加以证明;
(2)若AB=AD,以过点P的直线为轴,将四边形ABCD折叠,使点B、C分别落在点B′、C′上,且B′C′经过点D,折痕与四边形的另一交点为Q.
①在图2中作出四边形PB′C′Q(保留作图痕迹,不必说明作法和理由);
②如果∠C=60°,那么 ![]() 为何值时,B′P⊥AB.
为何值时,B′P⊥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
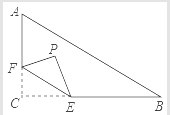
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,若点P能落在线段AB上,则线段CF长的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有三点A(a,0),B(b,0),C(1,3),且a,b满足|3b+a﹣2|+![]() =0
=0
(1)求A,B的坐标;
(2)在x负半轴上有一点D,使S△DOC=![]() S△ABC,求点D坐标:
S△ABC,求点D坐标:
(3)在坐标轴上是否还存在这样的点D,使S△DOC=![]() S△ABC仍然成立?若存在直接写出点D的坐标;若不存在,说明理由.
S△ABC仍然成立?若存在直接写出点D的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,CA平分∠BCD,∠B=60°,若AD=3,则梯形ABCD的周长为( ) 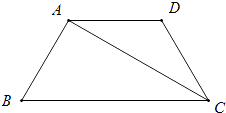
A.12 ![]()
B.15 ![]()
C.12
D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及平行四边形ABDC的面积![]() .
.
(2)在y轴上是否存在一点P,连接PA,PB,使![]() =2
=2![]() ,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
,若存在这样一点,求出点P的坐标,若不存在,试说明理由.
(3)点P是四边形ABCD边上的点,若△OPC为等腰三角形时,直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个直角三角形纸片OAB,其中∠AOB=90°,OA=2,OB=4.如图,将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB交于点C,与边AB交于点D.
(1)若折叠后使点B与点A重合,求点C的坐标.
(2)若折叠后点B落在边OA上的点为B′,是否存在点B′,使得四边形BCB′D是菱形?若存在,请说明理由并求出菱形的边长;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com