
【题目】如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上的三点.
(1)请画出△ABC关于x轴对称的△ABC;
(2)请写出B点关于y轴对称的点B2的坐标;若将点B向上平移h个单位,欲使其落在△A1B1C1内部,指出h的取值范围.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A. 对我市市民实施低碳生活情况的调查
B. 对我国首架大型民用飞机零部件的检查
C. 对全国中学生心理健康现状的调查
D. 对市场上的冰淇淋质量的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B、∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B、∠D的关系,不需要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ≈1.7,结果精确到个位).
≈1.7,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座仓库分别有农用车12辆和6辆.现在需要调往![]() 县10辆,需要调往
县10辆,需要调往![]() 县8辆,已知从甲仓库调运一辆农用车到
县8辆,已知从甲仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为40元和80元;从乙仓库调运一辆农用车到
县的运费分别为40元和80元;从乙仓库调运一辆农用车到![]() 县和
县和![]() 县的运费分别为30元和50元.
县的运费分别为30元和50元.
(1)设乙仓库调往![]() 县农用车
县农用车![]() 辆,求总运费
辆,求总运费![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若要求总运费不超过900元,问共有几种调运方案?试列举出来.
(3)求出总运费最低的调运方案,最低运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在等边△ABC中,点M是BC边上的任意一点(不含端点B,C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ACN=∠ABC.
【类比探究】
(2)如图②,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ACN=∠ABC还成立吗?请说明理由.
【拓展延伸】
(3)如图③,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
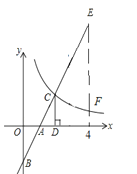
【题目】如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A,B两点,与双曲线y2=![]() (x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②
(x>0)交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:①当x>0时,y1随x的增大而增大,y2随x的增大而减小;②![]() ;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
;③当0<x<2时,y1<y2;④如图,当x=4时,EF=4.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某中学九年级学生在学习“直角三角形的边角关系”时,组织开展测量物体高度的实践活动.要测量学校一幢教学楼AB的高度如图所示,他们先在点C测得教学楼的顶部A的仰角为36.2°,然后向教学楼前进10米到达点D,又测得点A的仰角为45°.请你根据这些数据,求出这幢教学楼AB的高度.(结果精确到1米)
【参考数据:sin36.2°=0.59,cos36.2°=0.81,tan36.2°=0.73】

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com