
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴相交于点A(﹣2,0)和点B,与y轴相交于点C,顶点D(1,﹣ ![]() ).
).
(1)求抛物线的解析式;
(2)求四边形ACDB的面积;
(3)若(1)中的抛物线只进行上下平移或者左右平移,使平移后的抛物线与坐标轴仅有两个交点,请直接写出平移后的抛物线的关系式.

【答案】(1)y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() (2)15 (3)y=
(2)15 (3)y=![]() (x+3)2﹣
(x+3)2﹣![]()
【解析】试题分析:(1)由已知设二次函数为y=a(x﹣1)2﹣![]() ,把点A(-2,0)代入即可得;
,把点A(-2,0)代入即可得;
(2)先分别求得B、C的坐标,然后根据S四边形ACDB=S△AOC+S△DOC+S△ODB进行求解即可;
(3)当抛物线与坐标轴仅有两个交点,即图象顶点在x轴上或经过原点时即符合要求,根据此写出平移变换即可.
试题解析:(1)设二次函数为y=a(x﹣1)2﹣![]() ,
,
将点A(﹣2,0)代入上式得,
0=a(﹣2﹣1)2﹣![]() ,
,
解得:a=![]() ,
,
故y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ;
;
(2)令y=0,得0=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,
,
解得:x1=﹣2,x2=4,
则B(4,0),
令x=0,得y=﹣4,故C(0,﹣4),
S四边形ACDB=S△AOC+S△DOC+S△ODB=![]() ×2×4+
×2×4+![]() ×4×1+
×4×1+![]() ×4×
×4×![]() =15,
=15,
故四边形ACDB的面积为15;

(3)当抛物线与坐标轴仅有两个交点,即图象顶点在x轴上或经过原点时即符合要求,
①当抛物线顶点在x轴上时,将抛物线y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() 向上平移
向上平移![]() 个单位,y=
个单位,y=![]() (x﹣1)2;
(x﹣1)2;
②当抛物线经过原点时,将抛物线y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() 向上平移4个单位,y=
向上平移4个单位,y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() ,或将抛物线y=
,或将抛物线y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() 向右平移2个单位,y=
向右平移2个单位,y=![]() (x﹣3)2﹣
(x﹣3)2﹣![]() ;或将抛物线y=
;或将抛物线y=![]() (x﹣1)2﹣
(x﹣1)2﹣![]() 向左平移4个单位y=
向左平移4个单位y=![]() (x+3)2﹣
(x+3)2﹣![]() (写出一种情况即可).
(写出一种情况即可).


科目:初中数学 来源: 题型:
【题目】根据题意及解答过程填空:
如图所示,AB=10cm,D为AC的中点,DC=2cm,BE=![]() BC,求CE的长。
BC,求CE的长。
![]()
解:因为D为AC的中点,DC=2cm.
所以AC="_______DC=_______" cm.
由图可知:BC="______" -AC
="10" cm-____cm
=_______cm.
所以BE=![]() BC=______cm.
BC=______cm.
所以CE=BC-BE=_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(a,b)为第一象限内一点,且a<b.连结OA,并以点A为旋转中心把OA逆时针转90°后得线段BA.若点A、B恰好都在同一反比例函数的图象上,则![]() 的值等于___.
的值等于___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家在甲、乙两商场销售同一件商品所获得的利润分别为![]() ,(单位:元),
,(单位:元),![]() 与销售量
与销售量![]() (单位:件)的函数关系图象如图所示,试根据图像解决下列问题:
(单位:件)的函数关系图象如图所示,试根据图像解决下列问题:

(1)分别求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)现厂家分配该商品800件给甲商场、400件给乙商场,当甲、乙两商场售完这批商品后,厂家可获得总利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AD是△ABC的中线,E为AD的中点,过点A作AF∥BC交BE延长线于点F,连接CF.
(1)如图1,求证:四边形ADCF是平行四边形;
(2)如图2.连接CE,在不添加任何助线的情况下,请直接写出图2中所有与△BEC面积相等的三角形。

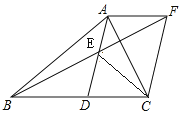
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽取本校部分同学,调查同学了解母亲生日日期的情况,分“知道、不知道、记不清”三种.下面图①、图②是根据采集到的数据,绘制的扇形和条形统计图.

请你要根据图中提供的信息,解答下列问题:
(1)求本次被调查学生的人数,并补全条形统计图;
(2)在图①中,求出“不知道”部分所对应的圆心角的度数;
(3)若全校共有1440名学生,请你估计这所学校有多少名学生知道母亲的生日?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起,友情提示:∠A=60°,∠D=30°,∠E=∠B=45°.
(1)①若∠DCB=45°,则∠ACB的度数为 .
②若∠ACB=140°,则∠DCE的度数为 .
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<90°且点E在直线AC的上方时,当这两块三角尺有一组边互相平行时,请直接写出∠ACE角度所有可能的值(不必说明理由).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com