
����Ŀ���Ķ����⣺��ͼ1�����������A1A2A3��An�ı�A2A3����ȡһ�����A2�غϵĵ�B2�������߶�A1B2Ϊ�����߶�A1A2���Ϸ������������A1B2B3��Bn�����������A1B2B3��Bn���������A1A2��An��λ��ͼ�Σ���A3��Ϊλ�����ģ�
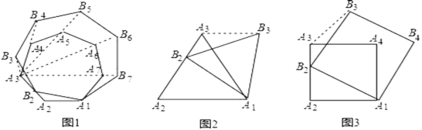
������֤����1����ͼ2��֪��������A1A2A3��λ��ͼ��Ϊ��������A1B2B3����֤�������ŵ�B2���˶�����B3A3A1�Ĵ�Сʼ�ղ��䣮
��ѧ˼������2����ͼ3��֪������A1A2A3A4��λ��ͼ��Ϊ������A1B2B3B4�����ŵ�B2���˶�����B3A3A4�Ĵ�Сʼ�ղ��䣿�����䣬�������B3A3A4�Ĵ�С�����ı䣬��˵�����ɣ�
���ɲ��룺��3����ͼ��1��������£����Բ����B3A3A4�Ĵ�С�Ƿ�ᷢ���ı䣿�����ı䣬���ú�n�Ĵ���ʽ��ʾ����B3A3A4�Ĵ�С��ֱ��д������������ı䣬��˵�����ɣ��ڡ�B3A3A4+��B4A4A5+��B5A5A6+��+��BnAnA1=�� �����ú�n�Ĵ���ʽ��ʾ��
���𰸡���1������������2�����䣬45������3���ٲ��䣬![]() ����
����![]()
��������
��1�����жϳ���A2A1B2�ա�A3A1B3�������õȱ������ε����ʼ��ɵó����ۣ�
��2�����жϳ���A3B2B3�ա�DA1B2�������������ε����ʼ��ɵó����ۣ�
��3�������жϳ���A3B2B3�ա�DA1B2��������������εı���Ⱥ�ÿ���ڽǼ��ɵó����ۣ������âٵĽ��ۺͷ������ɵó����ۣ�
�⣺��1��֤�����ߡ�A1A2A3����A1B2B3���������Σ�
��A1A2=A1A3��A1B2=A1B3����A2A1A3=��B2A1B3=60����
���A2A1B2=��A3A1B3��
���A2A1B2�ա�A3A1B3��
���B3A3A1=��A2=60����
���B3A3A1�Ĵ�С���䣻
��2����B3A3A4�Ĵ�С���䣬
���ɣ���ͼ���ڱ�A1A2��ȡһ��D��ʹA1D=A3B2������B2D��
���ı���A1A2A3A4��A1B2B3B4�������Σ�
��A1B2=B2B3����A1B2B3=��A1A2A3=90����
���A3B2B3+��A1B2A2=90������A2A1B2+��A1B2A2=90����
���A3B2B3=��A2A1B2��
���A3B2B3�ա�DA1B2��
���B2A3B3=��A1DB2��
��A1A2=A2A3��A1D=A3B2��
��A2B2=A2D��
�ߡ�A1A2A3=90����
���DA2B2�ǵ���ֱ�������Σ�
���A1DB2=135����
���B2A3B3=135����
�ߡ�A4A3A2=90����
���B3A3A4=45����
������B3A3A4�Ĵ�Сʼ�ղ��䣻
��3���١�B3A3B4�Ĵ�Сʼ�ղ��䣬���ɣ���ͼ1��
��A1A2��ȡһ��D��ʹA1D=A3B2��
����B2D��
�ߡ�A2A1B2=180������A1B2A2����A3B2B3=180������A1B2A2��
���A2A1B2=��A3B2B3��
��A1B2=B2B3��
���A3B2B3�ա�DA1B2��
���B2A3B3=A1DB2��
��A1A2=A2A3��A1D=A3B2��
��A2D=A2B2��
���A1DB2=![]() =90����
=90����![]()
���B3A3A4=��A1DB2����B2A3A4=90����![]() ��
��![]() =
=![]() ��
��
���ɢ�֪����B3A3A4=![]() ��
��
ͬ�ٵķ����ɵã���B4A4A5=![]() ��2����B5A5A6=
��2����B5A5A6=![]() ��3��������BnAnA1=
��3��������BnAnA1=![]() ����n��2����
����n��2����
��١�B3A3A4+��B4A4A5+��B5A5A6+��+��BnAnA1
=![]() +
+![]() ��2+
��2+![]() ��3+��
��3+��![]() ����n��2��=
����n��2��=![]() ��
��
�ʴ�Ϊ��![]() ��
��



 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ������ͼ�����������⣺
��1�������ax2+bx+c=0����������
��2��д������ʽax2+bx+c��0�Ľ⼯��
��3��д��y��x���������С���Ա���x��ȡֵ��Χ.
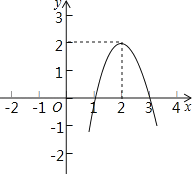
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������300ǧ�ף�һ��������һ���γ��Ⱥ�Ӽس���ʻ���ҵأ���ͼ���߶�OA��ʾ������ؾ���y��ǧ�ף���ʱ��x��Сʱ��֮��ĺ�����ϵ������OBCDA��ʾ�γ���ؾ���y��ǧ�ף���ʱ��x��Сʱ��֮��ĺ�����ϵ�������ͼ�����������⣺
��1�����γ��յ��ҵ�ʱ����ʱ���������ҵ��� ��ǧ�ף�
��2�����γ����������ʱ�����ʱx��ֵ��
��3����������ʻ�����У����γ���������20ǧ��ʱ����x��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
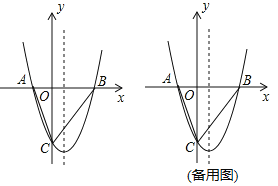
����Ŀ����ͼ��������y��x2+bx+c��x�ύ��A��B���㣬��y�ύ��C�㣬OA��2��OC��6������AC��BC��
��1���������ߵĽ���ʽ��
��2����D�������ߵĶԳ����ϣ�����ACD���ܳ���Сʱ�����D�����ꣻ
��3����E�ǵ����������������ϵĶ��㣬����CE��BE�����BCE��������ֵ����ʱ��E�����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ڽ��ڡ�O��AB��ֱ����OD��AC��AD=OC��
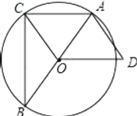
��1������B=30��ʱ�����ж��ı���OCAD����״��Ϊʲô��
��2������B���ڶ��ٶ�ʱ��AD���O���У���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() �����Բ��
�����Բ��![]() ��
��![]() ��ֱ������
��ֱ������![]() ���е�
���е�![]() ��
��![]() ��ֱ��
��ֱ��![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��![]() .
.
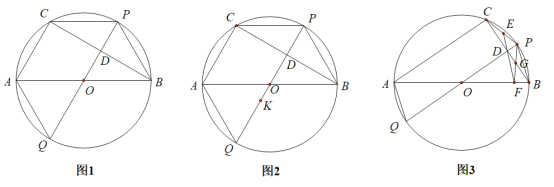
��1����ͼ1������![]() ���߶�
���߶�![]() ���е㣬��
���е㣬��![]() �Ķ�����
�Ķ�����
��2����ͼ2����![]() ��ȡһ��
��ȡһ��![]() ��ʹ
��ʹ![]() ����֤��
����֤��![]() ��
��
��3����ͼ3��ȡ![]() ���е�
���е�![]() ������
������![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ����
����![]() ����
����![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������:
����![]() ����
����![]() ��
��
�ڵ�![]() ʱ����
ʱ����![]() ����
����![]() ��
��
��ֱ����������б���ϵ����ߵ���б�ߵ�һ�룻
�ܾ��ε������Խ������.
����ԭ�������������Ϊ������ĸ����ǣ� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�Һ���λ�ڵ���P�Ķ������������80�����A�����������Ϸ�����һ��ʱ�����λ�ڵ���P����ƫ��30�������ϵ�B����
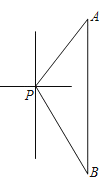
��1��������P��Χ50���ﷶΧ���а��������ִ�A����B����;�У��Ƿ��д���Σ�գ�
��2����������ÿСʱ30������ٶȴ�A����B�������жϺ����ܷ���5Сʱ�ڵ���B������˵�����ɣ����ο����ݣ�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��![]() ��2.45��
��2.45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
С���۲�һ����1��1�����ε�����ɵĵ���ͼ��ͼ��ˮƽ����ֱ�����������������ڵ��ľ��붼��1��������һ����Ȥ�����⣺����ͼ�г��ֵ����������˵��ڵ������һ����ֱ���߶Σ��������ڵ������ҵ�һ�㹹�촹ֱ��������������봹��֮�����ֵ��
��ش�
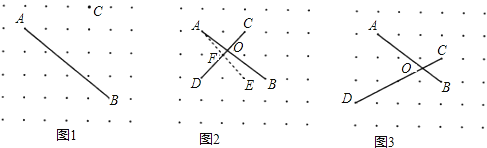
��1����ͼ1��A��B��C�ǵ����е������㣬���ڵ������ҵ���D�������߶�CD��ʹ��CD��AB��
��2����ͼ2���߶�AB��CD���ڵ�O��С���ڵ������ҵ��˵�E������AE��ǡ������AE��CD��E�������������е������߶Σ��Ϳ��Թ������������Σ����������ͼ����ܹ�ʹ����õ������
�����С�����㣺OC���� ��OF���� ����
�ο�С��˼������ķ�����������⣺
��3����ͼ3���߶�AB��CD���ڵ�O���ڵ������ҵ���E������AE������AE��CD��F�����㣺 OC���� ����OF���� ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com