
【题目】如图所示,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() .
.
(1)求抛物线对应的函数表达式;
(2)![]() 是线段
是线段![]() 上的任意一点,当
上的任意一点,当![]() 为等腰三角形时,求点
为等腰三角形时,求点![]() 的坐标.
的坐标.
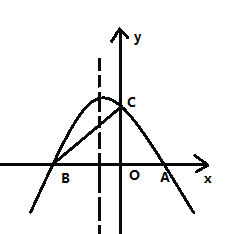
【答案】(1)y=![]() (x+
(x+![]() )2+
)2+![]() ;(2)(0,0)或(
;(2)(0,0)或(![]() -3,0)
-3,0)
【解析】
(1)根据抛物线的对称轴得到抛物线的顶点式,然后代入已知的两点理由待定系数法求解即可;
(2)首先求得点B的坐标,然后分BC=CM时,CM=BM时和BC=BM时,三种情况根据等腰三角形的性质求得点M的坐标即可.
解:(1)依题意,设抛物线的解析式为y=a(x+![]() )2+k, 由A(2,0),C(0,3)得
)2+k, 由A(2,0),C(0,3)得
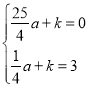 ,
,
解得: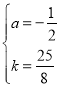 ,
,
∴抛物线的解析式为:y=![]() (x+
(x+![]() )2+
)2+![]() ;
;
(2)当y=0时,有![]() (x+
(x+![]() )2+
)2+![]() =0.
=0.
解得:x1=2,x2=-3;
∴B(-3,0) ,
∵△MBC为等腰三角形,则
①当BC=CM时,M在线段BA的延长线上,不符合题意,即此时点M不存在;
②当CM=BM时,
∵M在线段AB上,
∴M点在原点O上,即M点坐标为(0,0);
③当BC=BM时,在Rt△BOC中,BO=CO=3,
由勾股定理得BC=![]() ,
,
∴BM=![]() .
.
∴M点坐标为(![]() ,0).
,0).
综上所述,M点的坐标为(0,0)或(![]() ,0).
,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为落实“垃圾分类”,环卫部门要求垃圾要按A,B,C三类分别装袋,投放,其中A类指废电池,过期药品等有毒垃圾,B类指剩余食品等厨余垃圾,C类指塑料,废纸等可回收垃圾.甲投放了一袋垃圾,乙投放了两袋垃圾,这两袋垃圾不同类.
(1)直接写出甲投放的垃圾恰好是A类的概率;
(2)求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下面的几何探究过程:
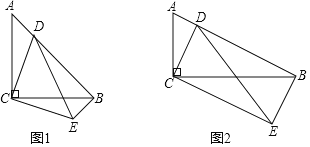
(1)观察填空
如图1,在Rt△ABC中,∠C=90°,AC=BC=4,点D为斜边AB上一动点(不与点A,B重合),把线段CD绕点C顺时针旋转90°得到线段CE,连DE,BE,则
①∠CBE的度数为____________;
②当BE=____________时,四边形CDBE为正方形.
(2)探究证明
如图2,在Rt△ABC中,∠C=90°,BC=2AC=4,点D为斜边AB上一动点(不与点A,B重合),把线段CD绕点C顺时针旋转90°后并延长为原来的两倍得到线段CE,连DE,BE则:
①在点D的运动过程中,请判断∠CBE与∠A的大小关系,并证明;
②当CD⊥AB时,求证:四边形CDBE为矩形
(3)拓展延伸
如图2,在点D的运动过程中,若△BCD恰好为等腰三角形,请直接写出此时AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴分别交于
与x轴分别交于![]() ,
,![]() 两点,与y轴交于点C.
两点,与y轴交于点C.
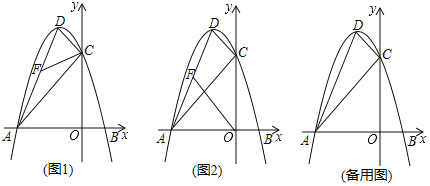
(1)求抛物线的表达式及顶点D的坐标;
(2)点F是线段AD上一个动点.
①如图1,设![]() ,当k为何值时,
,当k为何值时,![]() .
.
②如图2,以A,F,O为顶点的三角形是否与![]() 相似?若相似,求出点F的坐标;若不相似,请说明理由.
相似?若相似,求出点F的坐标;若不相似,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 和一次函数
和一次函数![]() .
.
(1)当t=0时,试判断二次函数![]() 的图象与x轴是否有公共点,如果有,请写出公共点的坐标;
的图象与x轴是否有公共点,如果有,请写出公共点的坐标;
(2)若二次函数![]() 的图象与x轴的两个不同公共点,且这两个公共点间的距离为8,求t的值;
的图象与x轴的两个不同公共点,且这两个公共点间的距离为8,求t的值;
(3)求证:不论实数t取何值,总存在实数x,使![]() ≥
≥![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为1的正方形纸片ABCD折叠,使点B的对应点M落在边CD上(不与点C、D重合),折痕为EF,AB的对应线段MG交AD于点N.以下结论正确的有( )①∠MBN=45°;②△MDN的周长是定值;③△MDN的面积是定值.

A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
与直线![]() 相交于
相交于![]() ,
,![]() 两点,且抛物线经过点
两点,且抛物线经过点![]()
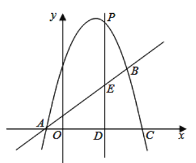
(1)求抛物线的解析式.
(2)点![]() 是抛物线上的一个动点(不与点
是抛物线上的一个动点(不与点![]() 点
点![]() 重合),过点
重合),过点![]() 作直线
作直线![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当
.当![]() 时,求
时,求![]() 点坐标;
点坐标;
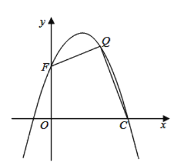
(3)如图所示,设抛物线与![]() 轴交于点
轴交于点![]() ,在抛物线的第一象限内,是否存在一点
,在抛物线的第一象限内,是否存在一点![]() ,使得四边形
,使得四边形![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】廊桥是我国古老的文化遗产.如图,是某座抛物线型的廊桥示意图,已知抛物线的函数表达式为![]() ,为保护廊桥的安全,在该抛物线上距水面
,为保护廊桥的安全,在该抛物线上距水面![]() 高为8米的点
高为8米的点![]() 、
、![]() 处要安装两盏警示灯,则这两盏灯的水平距离
处要安装两盏警示灯,则这两盏灯的水平距离![]() 是____米.
是____米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com