
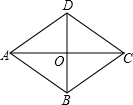
 解:由直角三角形的三边关系可得:AO2+BO2=25,又有根与系数的关系可得:AO+BO=-2m-1,AO•BO=m2-4,
解:由直角三角形的三边关系可得:AO2+BO2=25,又有根与系数的关系可得:AO+BO=-2m-1,AO•BO=m2-4,

科目:初中数学 来源: 题型:
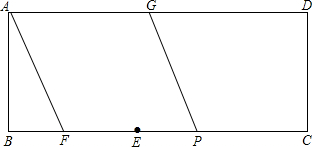 矩形ABCD,AD=5,AB=BE=2,点F是BE上的动点,以AF为一边菱形AFPG交BC于P点交AD于G点,如果分别以GP、DC为直径作圆,且使两圆外切,求BF的值.
矩形ABCD,AD=5,AB=BE=2,点F是BE上的动点,以AF为一边菱形AFPG交BC于P点交AD于G点,如果分别以GP、DC为直径作圆,且使两圆外切,求BF的值.查看答案和解析>>
科目:初中数学 来源: 题型:
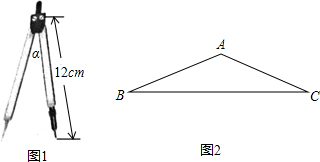 如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为12cm,最大张角150°,你能否画出一个半径为20cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
如图1,圆规两脚形成的角α称为圆规的张角.一个圆规两脚均为12cm,最大张角150°,你能否画出一个半径为20cm的圆?请借助图2说明理由.(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com